Question

L and M are the mid points of two equal chords AB and CD and O is the centre of the circle. Prove that
$
  \left( i \right)\angle OLM = \angle OML \\
  \left( {ii} \right)\angle ALM = \angle CML \\
 $

Answer 1

Hint: Here we will proceed by using the property of circle i.e. the line joining the centre of the midpoint of a chord is perpendicular to the chord to show the perpendiculars to the triangle. Then we will use other properties of the circle to prove the statement.

Complete step-by-step answer:

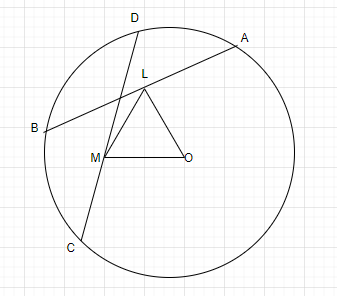
As we are given that AB and CD are two equal chords of a circle with centre O.
And L is the midpoint of AB and M is the midpoint of CD.
We have to prove that $
  \left( i \right)\angle OLM = \angle OML \\
  \left( {ii} \right)\angle ALM = \angle CML \\
 $
Proof – As L is the midpoint of chord AB of circle with centre O.
We know that the line joining the centre of the midpoint of a chord is perpendicular to the chord.
Which implies that-
$OL \bot AB$ and $OM \bot CD$
AB = CD (given)
By using the property of circle i.e. equal chords are equidistant from the centre, we get-
OL = OM
In $\vartriangle OLM,$
OL = OM (proved above)
 $\angle OLM = \angle OML$…….. (1)
 (angle opposite to equal sides of a triangle are equal)
$\angle OLA = \angle OMC$ …………. (2)
( Each angle is ${90^ \circ }$)
On adding equations 1 and 2,
We get-
$\angle OLM + \angle OLA = \angle OML + \angle OMC$
$\angle ALM = \angle CML$ ……….. (3)
From equation 1 and 3, we proved that-
$\angle OLM = \angle OML$ and $\angle ALM = \angle CML$

Note – In order to solve this type of question we must know all the properties of circle and triangle as here in this question we used two properties of circle and also the property of triangle. Also no step should be omitted as every step involved an important operation.