Question

How do you know that the given angles are supplementary?

Answer 1

Hint: For solving this question, we must know about the supplementary angles. The angles that measure up to 180 degrees are termed as Supplementary angles. If the given two angles are supplementary then their adjacent or their non-shared sides generally form a straight line.

Complete step-by-step answer:
The angles are said to be supplementary only when –
One of its angles is an acute angle while the other angle is an obtuse angle.
Both of the angles are right angles.
This, means that $ \angle A + \angle B = {180^0} $
For better understanding we will see the next example.

About the supplementary angle theorem
The supplementary angle theorem suggests that if the given two angles are supplementary to the same angle, then these two angles are said to be congruent.
Properties of Supplementary angles:
I.Given two angles are supplementary angles only when their sum is 180°.
II.These two angles must make together a straight line, but the angles need not be together.
III.In supplementary angles the “S” stands for the “Straight” line. This means they must form 180°.
Some of the basic examples of supplementary angles are as follows:
 $ \bullet \,\,\,{132^0} + \,\,{48^0} = \,{180^0} $
 $ \bullet \,\,\,{90^0} + \,\,{90^0} = \,{180^0} $
  $ \bullet \,\,\,{110^0} + \,\,{70^0} = \,{180^0} $
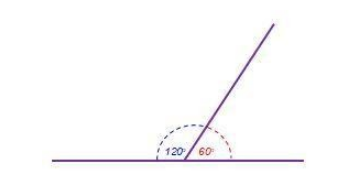
  $ \bullet \,\,\,{120^0} + \,\,{60^0} = \,{180^0} $
How to find the Supplementary angles:-
We generally know that the sum of two supplementary angles is $ {180^0} $
Hence, $ \angle A + \angle B = {180^0} $
Or $ \angle A = {180^0} - \angle B $

Note: For solving this question, we must have the basic knowledge about the supplementary angles, and some basic mathematical formulae. The importance of supplementary angles is that they can be used to find the other angles.