Question

How do you know if \[y=3x-2\] is a function?

Answer 1

Hint: A function is defined as a relationship which has one-one property, it means that for every value of an independent variable (in our case x), it should have a unique value of dependent variable (in our case x). We can verify this condition by drawing a vertical line on the graph of the equation. If the vertical line crosses the graph of the equation more than one time, then the given equation cannot be a function.

Complete step by step answer:
The degree of an equation is the highest power to which the independent variable of the equation is raised. The degree of an equation is always an integer. We can say whether the equation is linear or quadratic or any other polynomial equation by using the degree.
We are given \[y=3x-2\]. As the highest power of the variable in this equation is 1, the degree of this equation is also 1. From this, we can say that it is a linear equation, and hence its graph should be a straight line.
We can plot the graph of given equation of straight line as follows,

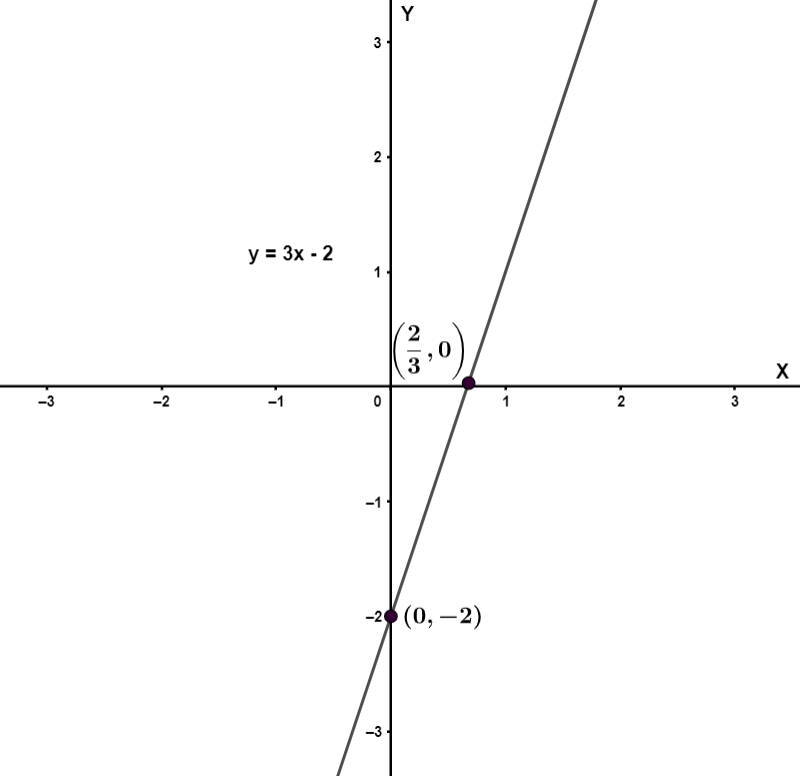
We can see that the graph has a positive slope at each point, thus its equation is always increasing. Hence, a vertical line drawn at any point will cross the graph only once. Hence, we can say that \[y=3x-2\] is a function.

Note: We will see an example of an equation which is not a function, to make things clearer.
Let’s take the equation, \[x={{y}^{2}}\]. The graph of the function is as follows,

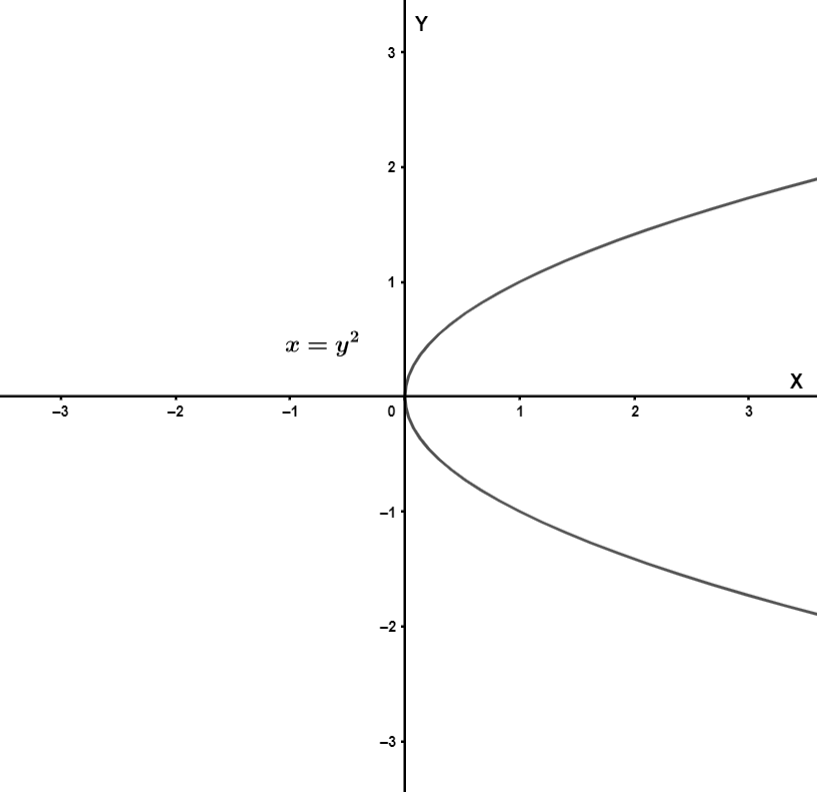
As we can see that a vertical line drawn on the positive sides of the X-axis will cross the graph more than once. Thus, it is not a function.