Question

How do we know if two lines are parallel in three-dimensional space?

Answer 1

Hint: We start solving the problem by choosing any two points on the given points and then recall the fact that the Direction Ratios of the line are found by subtracting the corresponding coordinates of the chosen two points. We then recall the fact that the Direction Ratios of both the lines are to be multiples of each other in order to have the lines parallel to each other which is the required answer.

Complete step by step answer:
According to the problem, we have to tell the rules to check whether the two given lines in three-dimensional space are parallel.
$\Rightarrow$ We first choose two points on each line for example $ A\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right) $ and $ B\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right) $ .
$\Rightarrow$ We then perform the subtraction operation between the corresponding coordinates between these two points to get the Direction Ratios of the line i.e., $ \left( {{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}},{{z}_{2}}-{{z}_{1}} \right) $ for both the lines.

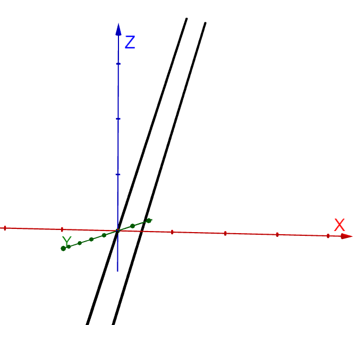
$\Rightarrow$ If we get the two Direction Ratios are multiples of each other, then the given lines are parallel.
 $ \, therefore, $ We have found that the Direction ratios of both the lines has to be multiples of each other in order to find the lines parallel.


Note:
We can also check whether the given lines are parallel as shown below-
$\Rightarrow$ If we have the direction ratios of both the given lines are $ \left( {{a}_{1}},{{b}_{1}},{{c}_{1}} \right) $ , $ \left( {{a}_{2}},{{b}_{2}},{{c}_{2}} \right) $ . Then the condition for the lines to be parallel is $ \dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}} $ . Similarly, we can expect problems to find the conditions for the lines to become perpendicular and skew lines in three-dimensional space.