Question

How will you know if the center of a circle is tangent to y axis?
 (a) y coordinate equals absolute value of radius
(b) x coordinate equals absolute value of radius
(c) x coordinate = y coordinate
(d) None of these

Answer 1

Hint: In this problem, we are trying to find a condition when the center of a circle is tangent to y axis. A condition can be considered to be true and checked if it is working or not. So, as we are talking about a tangent to y axis, we will start by checking it with the x coordinate. As it satisfies with our given condition, we have our solution.

Complete step-by-step solution:
According to the question, we are to find the condition where the centre of a circle is tangent to y axis.
Let us consider, a circle is tangent to the y axis if and only if the absolute value of its x coordinate equals the radius is the condition where this holds.
Let us consider it with an example.
If we have a point ( 3, 5) as a centre and the radius is exactly 3, then the circle will reach the point (0, 5) at its leftmost point.
The above condition can be shown graphically as:

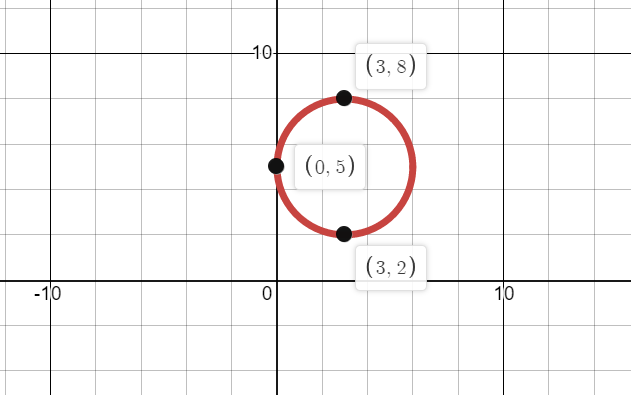
Again, if we have the centre say, ( - 5, 9) and the radius is exactly 5, then also the circle can not go to the right more than the point ( 0, 9).
In the formula, if we write the equation of the circle, we get,
${{\left( x-{{x}_{0}} \right)}^{2}}+{{\left( y-{{y}_{0}} \right)}^{2}}={{r}^{2}}$
Then if, $\left| {{x}_{0}} \right|=r$ , we will have that the circle would be tangent to the y axis.
Hence, the solution is, (b) x coordinate equals absolute value of radius.

Note: If a circle is tangent to the y-axis at (3,0), this means it touches the y-axis at that point. Given these two points, we can determine the center and the radius of the circle. The center of the circle must be equidistant from any of the points on the circumference. This means that both (0,3) and (3,0) are the same distance from the center. If we draw these points on a coordinate plane, it becomes apparent that the center of the circle must be (3,3).