Question

Kichu and Sachu were on a morning walk. On reaching a junction, Kichu moved exactly eastward and Sachu moved exactly northwards. Sachu was at a speed of 30 metres per minute more than Kichu. After 10 minutes the shortest distance between them was 1.5 kilometres. Draw a rough figure showing the position of Kichu, Sachu and the junction.
Calculate the distance covered by each. Find their respective speeds. \[\]

Answer 1

Hint: We denote the junction by O, the position of Kichu eastward after 10 minute of journey as by B and the position of Sachu northward after 10 minute of journey as by A. We draw the figure and join AB. We assume the speed of Kichu as $x$ km/minute which gives us the speed of Sachu as $\left( x+30 \right)$ km/min. We use speed-distance relation and conclude from the figure that $OA=300+10x,OB=10x$ and given AC=1.5km. We use the Pythagoras theorem in the right angled triangle OAB and solve for $x$. We find the required values. \[\]

Complete step-by-step answer:
We are given the question that Kichu and Sachu were on a morning walk. On reaching a junction, Kichu moved exactly eastward and Sachu moved exactly northwards. Let the junction be denoted by the position O.
We are further given that Sachu was at a speed of 30 metres per minute more than Kichu. After 10 minutes the shortest distance between them was 1.5 kilometres. Let us denote the postion of Sachu be A and Kichu be B. We have the diagram showing the position of Kichu B , Sachu A and the junction O. \[\]
 

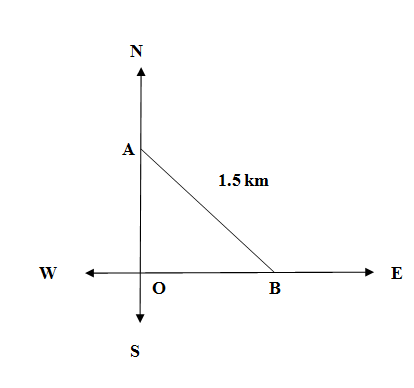
Let us assume the speed of Kichu as $x$ km/minute. Hence the speed of Sachu is $\left( x+30 \right)$ km/min. The time taken by both of them is 10 minutes. So the distance covered by Kichu is$10\times x=10x$ and the distance covered by Sachu is $10\times \left( 30+x \right)=300+10x$. So we have,
\[OA=300+10x,OB=10x\]
We are given the question to find the shortest distance between A and B that is $AB=1.5\text{km}=1.5\times 1000\text{m}=1500\text{m}$. We know from Pythagoras theorem that “In a right-angled triangle the square of the hypotenuse is the sum of squares of the other two sides.” We observe the right- angled triangle OAB and find that AB is the hypotenuse. So we have,
\[\begin{align}
  & A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}} \\
 & \Rightarrow {{1500}^{2}}={{\left( 300+10x \right)}^{2}}+{{\left( 10x \right)}^{2}} \\
 & \Rightarrow 2250000=9000+600x+200{{x}^{2}} \\
 & \Rightarrow 2{{x}^{2}}+60x+900=22500 \\
 & \Rightarrow 2{{x}^{2}}+60x-21600=0 \\
\end{align}\]
Let us divide the above equation and have,
\[\Rightarrow {{x}^{2}}+30x-10800=0\]
We solve the above quadratic equation by splitting the middle term method and have,
\[\begin{align}
  & \Rightarrow {{x}^{2}}+120x-90x-10800=0 \\
 & \Rightarrow x\left( x+120 \right)-90\left( x+120 \right)=0 \\
 & \Rightarrow \left( x+120 \right)\left( x-90 \right)=0 \\
 & \Rightarrow x=-120,90 \\
\end{align}\]
We reject the root of$x=-120$ for speed and conclude that the speed of Kichu was $x=90$m/min. Hence the speed of Sachu was $30+x=30+90=120$m/min. The distance travelled by Kichu is $10x=10\times 90=900$m and the distance travelled by Sachu is 10 $10\left( 30+x \right)=10\times \left( 30+90 \right)=1200$m. \[\]

Note: We note that speed is always a positive scalar quantity and that is the reason we rejected $x=-120$ but velocity is a vector that can be negative. We can alternatively solve by first finding the coordinate of the position of Sachu and Kichu as $A\left( 0,300+10x \right)$, $B\left( 10x,0 \right)$ and then using distance formula between any two point on a plane $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.