Question

Kamal and Monika appeared for an interview for two vacancies. The probability of Kamal’s selection is $\dfrac{1}{3}$ and that of Monika’s selection is $\dfrac{1}{5}$. Find the probability that none of them will be selected.

Answer 1

Hint: The sum of probability of something to happen and the same thing to not happen is always equal to 1.
Let us assume that we are tossing a coin then the probability of heads as outcome is $\dfrac{1}{2}$and probability of tail outcome is also $\dfrac{1}{2}$.
Probability of favourable outcomes + Probability of unfavourable = 1.
Here in our assumed case also P(H) + P(T) = 1.
Similarly, we subtract the probability of Kamal and Monica being selected for the interview from 1 inorder to get the probability of none of them being selected.

Complete step-by-step answer:

It is given in the question that Kamal and Monika are appearing for an interview for two vacancies.

The probability of Kamal’s selection is $\dfrac{1}{3}$ and the probability of Monika’s selection is $\dfrac{1}{5}$.

Now, we have to find the probability that none of them will be selected.

The figure below shows the probability of Monika and Kamal passing or failing in the interview respectively.

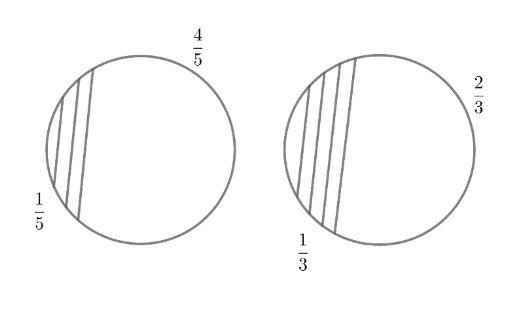
In the figure, the shaded area shows the probability that Monika and Kamal will pass and the unshaded area shows the probability that they may fail.

To calculate the probability that none of them will pass this interview. Then we have to find it by the chances that do not favour them in the interview.

We will calculate for Kamal’s probability that he may not pass in his interview.
So, we know that the sum of probability of favourable outcomes and probability of unfavourable outcomes is equal to 1.
Or $P\left( F \right)+P\left( F \right)'=1.............\left( 1 \right)$

Here, $P\left( F \right)$ is the favourable probability and $P\left( F \right)'$is the unfavourable probability.

So, for Kamal $P\left( F \right)$ is $\dfrac{1}{3}$ as it is given in the question.

So, on putting the value of $P\left( F \right)$ as $\dfrac{1}{3}$ in equation (1), we will get $P\left( F \right)'$which is the probability of Kamal not being selected.
$\begin{align}
  & \Rightarrow P\left( F \right)+P\left( F \right)'=1 \\
 & \Rightarrow \dfrac{1}{3}+P\left( F \right)'=1 \\
 & \Rightarrow P\left( F \right)'=1-\dfrac{1}{3} \\
 & \Rightarrow P\left( F \right)'=\dfrac{3-1}{3} \\
 & \Rightarrow P\left( F \right)'=\dfrac{2}{3} \\
\end{align}$

So, the probability that Kamal may fail in his interview is $\dfrac{2}{3}$.

Also,
$\begin{align}
  & P\left( F \right)+P\left( F \right)'=1 \\
 & or \\
 & \dfrac{1}{3}+\dfrac{2}{3}=1 \\
\end{align}$
Similarly, we will now calculate Monika’s probability that she may not pass in her interview.
So, for Monika $P\left( F \right)$ is $\dfrac{1}{5}$ as it is given in the question.
On putting the value of $P\left( F \right)$ as $\dfrac{1}{5}$ in equation (1), we get,
$\begin{align}
  & \Rightarrow P\left( F \right)+P\left( F \right)'=1 \\
 & \Rightarrow \dfrac{1}{5}+P\left( F \right)'=1 \\
 & \Rightarrow P\left( F \right)'=1-\dfrac{1}{5} \\
 & \Rightarrow P\left( F \right)'=\dfrac{5-1}{5} \\
 & \Rightarrow P\left( F \right)'=\dfrac{4}{5} \\
\end{align}$

So, now we have $P\left( F \right)'$ for Kamal is $\dfrac{2}{3}$ and $P\left( F \right)'$ for Monika is $\dfrac{4}{5}$.

Now, we will calculate the probability that none of them will be selected in the interview.
So, the probability that none of them will be selected in the interview = $P\left( F \right)'$ for Kamal x $P\left( F \right)'$ for Monika.

As we have $P\left( F \right)'$ for Kamal is $\dfrac{2}{3}$ and $P\left( F \right)'$ for Monika is $\dfrac{4}{5}$.

So, putting $P\left( F \right)'$ of Kamal and Monika in formula, we get
P(none of them selected) $=\dfrac{2}{3}\times \dfrac{4}{5}$
$\begin{align}
  & =\dfrac{2\times 4}{3\times 5} \\
 & =\dfrac{8}{15} \\
\end{align}$

Thus, the probability that both of them will be rejected in the interview is $\dfrac{8}{15}$.

Note: In this type of question always use the formula $P\left( F \right)+P\left( F \right)'=1$. You can also solve this question by using the concept of sets.
$P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right)$

$\begin{align}
  & P\left( A\cup B \right)=P\left( A \right)+P\left( B \right)-P\left( A\cap B \right) \\
 & 1=\dfrac{1}{3}+\dfrac{1}{5}-P\left( A\cap B \right) \\
\end{align}$
$P\left( A\cap B \right)$ is the probability that at least one of them will be selected.
$\begin{align}
  & 1-\dfrac{1}{3}-\dfrac{1}{5}=-P\left( A\cap B \right) \\
 & P\left( A\cap B \right)=\dfrac{7}{15} \\
\end{align}$
So, $P\left( A\cup B \right)-P\left( A\cap B \right)=1-\dfrac{7}{15}=\dfrac{8}{15}$