Question

Justify the statement – “Uniform circular motion is an accelerated motion “. Hence derive an expression for the centripetal acceleration of an object in a uniform circular motion in a plane.

Answer 1

Hint: Uniform circular motion in a plane means that the angular velocity of the particle undergoing circular motion is constant with time. One should always take care of the difference between scalar and vector quantity. Speed is a scalar quantity and on the other, velocity is a vector quantity. If the speed is constant, it doesn’t imply that the acceleration is zero but if the velocity is constant, it always implies that acceleration is zero or motion is non-accelerated.

Formula used:
$a= \dfrac{dv}{dt}$, $v=R \omega$

Complete step by step answer:
To understand the statement mathematically, let’s consider a particle undergoing circular motion with angular speed $\omega$ and radius ‘R’.

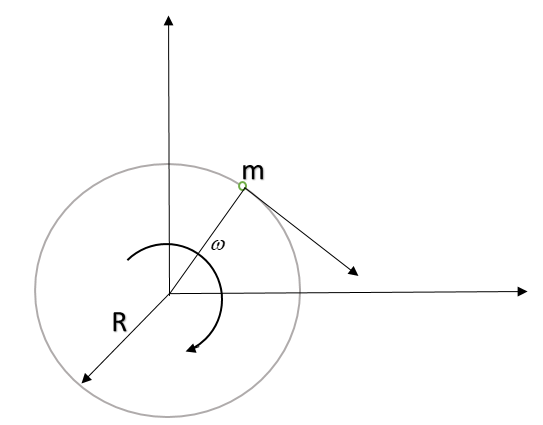
Starting from t=0, the angle turned by the particle after ‘t’ time will be $\omega t$ as shown in the figure below.

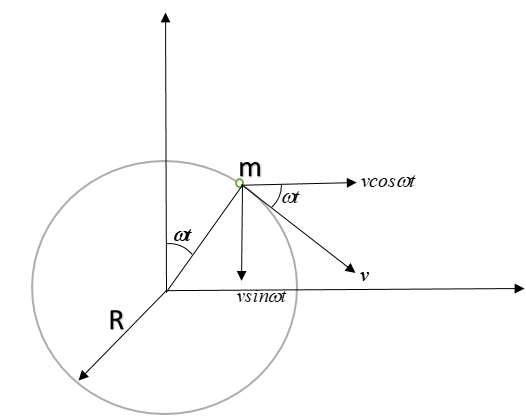
Let the magnitude of linear velocity of the particle be ‘$v$’ that is equal to $R \omega$. Hence resolving the velocity into x and y components, so: $\vec { v } =\quad (vcos\omega t\hat { )i } -(vsin\omega t)\hat { j }$
To find the acceleration of the particle, let's differentiate the velocity expression.
$a= \dfrac{dv}{dt}$
$a= \dfrac{d((vcos\omega t\hat { )i } -(vsin\omega t)\hat { j })}{dt}$ = $v \omega (-sin \omega t) \hat i - v \omega (cos \omega t) \hat j$ = $-v \omega (sin \omega t \ \hat i+cos \omega t \ \hat j)$
Putting $v=R \omega$, we get
 $\vec a = -\omega R^2 ( sin \omega t\ \hat i + cos \omega t\ \hat j)$
Hence we can clearly see that acceleration is non zero. Hence uniform circular motion is accelerated motion. So, the statement is justified.
Expression for centripetal acceleration of a body undergoing circular motion:
As we derived $\vec a = -\omega R^2 ( sin \omega t\ \hat i + cos \omega t\ \hat j)$
To find the magnitude:
$|\vec a| = \omega R^2 \sqrt{(sin \omega t)^2 + (cos \omega t)^2}$ = $\omega R^2$ [ $sin^2 \theta + cos^2 \theta = 1$]
Hence centripetal acceleration is $\omega R^2$.

Note:
As we derived the expression for the centripetal acceleration of the body undergoing uniform circular motion, we can see that the magnitude of this acceleration is constant with time. One should always analyze the quantities with their directions and magnitude separately. For example, the magnitude of centripetal acceleration is $\omega R^2$ but its direction is radially inwards (along the string). In short, we can say that the string is providing necessary centripetal force so that the particle can undergo circular motion.