Question

Jiya walks 6km due East and then 8km due North. How far is she from the starting place?

Answer 1

Hint: In the given question, we are provided with the information that contains the movement of Jiya with respect to direction and then we are being asked to find the distance she has moved from the initial point where she was standing to the final position where she reached. Using a figure will give the answer quickly as it would help to visualize her position quickly.

Complete step-by-step solution:
In the given question, we are given that Jiya walks 6km in East and 8km in North, now we need to find the distance between initial position and final position of Jiya.
From the figure, we can see that Jiya is standing at A. Therefore, A is the initial position of Jiya and then from there she travels 6km in East that is she reaches point C and then she moves 8km to North that is she reaches point B.
In the figure, AC is 6km towards East and BC is 8km towards North.
 

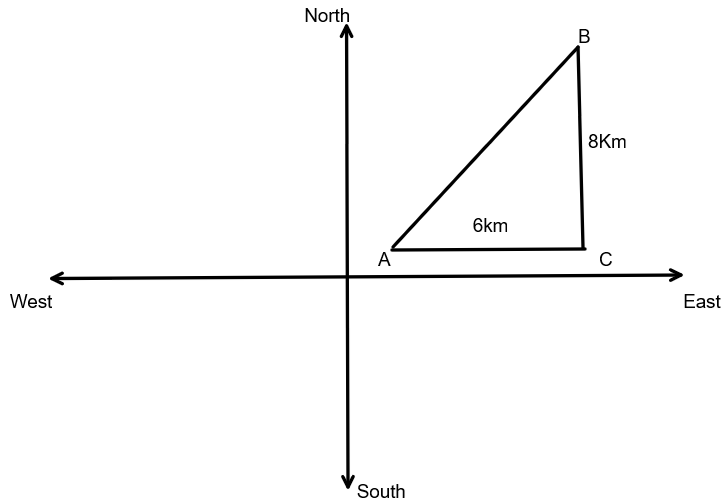
Now, we need to find the distance between the initial position and final position so that we can clearly see from the figure that it is equal to distance AB which is the hypotenuse of the right angled triangle ACB.
Therefore, $A{{B}^{2}}=A{{C}^{2}}+C{{B}^{2}}$ and now substituting the values we get, $\begin{align}
  & A{{B}^{2}}={{6}^{2}}+{{8}^{2}} \\
 & \Rightarrow A{{B}^{2}} = 36+64 \\
 & \Rightarrow A{{B}^{2}} = 100 \\
\end{align}$
Therefore, the distance between the initial and final position is 10km.

Note: In such questions we mainly are not aware of how to mark the direction in the figure and hence led to wrong interpretation of the distance and direction. So, we need to be careful while marking the direction and the distance in a particular direction. Rest all is very direct in this question. Also, we need to use distance formulas.