Question

James had \[4\dfrac{3}{4}\] feet of rope. He plans to cut off \[1\dfrac{1}{2}\] feet from the rope. How much rope will be left?

Answer 1

Hint: Here we just need to use a simple conversion method of fractions. We will convert mixed fractions into improper fractions and then in order to find the rope left we will subtract the length of rope James cut off from the total length of rope he had. This will be the answer to the question above.

Complete step by step solution:
Given the total length of rope is \[4\dfrac{3}{4}\] feet.
Now convert this mixed fraction into improper.
 \[4\dfrac{3}{4} = \dfrac{{19}}{4}\]
Now James cut off \[1\dfrac{1}{2}\] feet.
 \[1\dfrac{1}{2} = \dfrac{3}{2}\]
Now we need to make the denominator the same so as to subtract the ratios. So multiply the numerator and denominator by 2 to the cut part of the rope.
 \[\dfrac{3}{2} \times \dfrac{2}{2} = \dfrac{6}{4}\]
Now the part left after cutting will be given by,

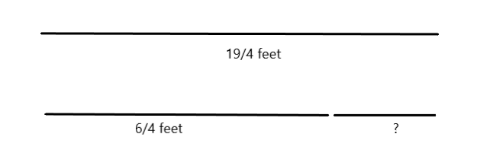
 \[\dfrac{{19}}{4} - \dfrac{6}{4} = \dfrac{{13}}{4}\]
This is the remaining part of the rope. And to write the same in the mixed fraction form we can write it as,
 \[\dfrac{{13}}{4} = 3\dfrac{1}{4}\] feet
Therefore, the remaining part of the rope is \[3\dfrac{1}{4}\] feet.

Note: Here note that converting into improper fractions will help the calculations to be easy. But it does not mean that we cannot use mixed fractions directly. We can use them as well. Also when we write the answer like in multiple questions if then observe the options whether they are in mixed fractions or are in improper fraction.
If mixed fraction is converted into improper then, \[a\dfrac{b}{c} = \dfrac{{c \times a + b}}{c}\]