Question

It is given that $\vartriangle ABC \sim \vartriangle PQR$ with $\dfrac{{BC}}{{PQ}} = \dfrac{1}{3}$. Then $\dfrac{{ar\vartriangle PQR}}{{ar\vartriangle BCA}}$ is equals to
A.9
B.3
C.31
D.91

Answer 1

Hint: In this question, we need to determine the ratio of the area of the triangle PQR and the triangle BCA such that the ratio of sides BC and PQ is given as 3:1. For this, we will use the property of the similar triangle, which states that the ratio of the area of the similar triangles is equivalent to the square of the ratio of the corresponding sides of the triangles.

Complete step-by-step answer:
Two triangles are said to be similar if their corresponding angles are congruent, and the corresponding sides are in proportion. In other words, similar triangles are the same shape but not necessarily the same size. The triangles are congruent if, in addition to this, their corresponding sides are of equal length.

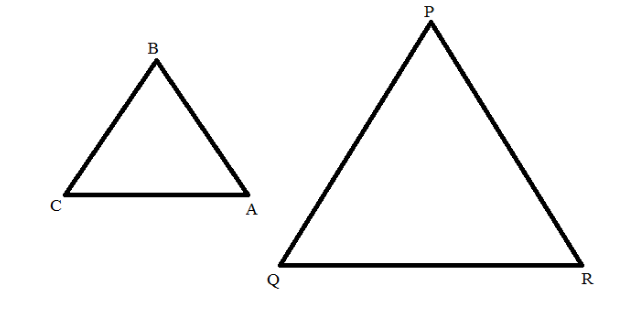
Following the property of the similar triangles, which states that the ratio of the area of the similar triangles is equivalent to the square of the ratio of the corresponding sides of the triangles. Mathematically, if the triangles ABC and PQR are similar $\left( {\vartriangle ABC \sim \vartriangle PQR} \right)$, then, $\dfrac{{ar\vartriangle ABC}}{{ar\vartriangle PQR}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2} = {\left( {\dfrac{{BC}}{{QR}}} \right)^2} = {\left( {\dfrac{{CA}}{{RP}}} \right)^2}$
Here, the triangle ABC is similar to the triangle PQR and the ratio of the sides of BC and PQ is given as 1:3,i.e., $\dfrac{{BC}}{{PQ}} = \dfrac{1}{3}$ or $\dfrac{{PQ}}{{BC}} = \dfrac{3}{1} - - - - (i)$
Hence, the ratio of the area of the triangle PQR and the area of the triangle ABC is given as the square of the ratio of the corresponding sides of the triangles. So, we can write
$
  \dfrac{{ar\vartriangle PQR}}{{ar\vartriangle BCA}} = {\left( {\dfrac{{PQ}}{{BC}}} \right)^2} \\
   = {\left( {\dfrac{3}{1}} \right)^2} \\
   = \dfrac{9}{1} \\
   = 9:1 \\
 $
Hence, $\dfrac{{ar\vartriangle PQR}}{{ar\vartriangle BCA}} = 9$
Option A is correct.
So, the correct answer is “Option A”.

Note: Nomenclature of similar triangles plays an important such as, $\dfrac{{ar\vartriangle ABC}}{{ar\vartriangle PQR}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2} = {\left( {\dfrac{{BC}}{{QR}}} \right)^2} = {\left( {\dfrac{{CA}}{{RP}}} \right)^2}$. Here we can see that the positions of the letters (vertex) in the nomenclature of the triangles are strictly followed while writing the ratios of the sides.