Question

It is given that $\vartriangle ABC \cong \vartriangle RPQ$. Is it true to say that $BC = QR$? If true then enter 1 else, enter 0.

Answer 1

Hint: Start by writing down the corresponding parts of the given congruent triangles. Compare the given sides and notice whether the given pair of sides is a corresponding pair of sides or not. If it is, then the given statement is correct. If it is not, then the given statement is false.

Complete step-by-step answer:
It is given that $\vartriangle ABC \cong \vartriangle RPQ$. To answer this question, we should first understand the basic definition of Congruency of triangles.
What is congruence of triangles?
Two triangles are said to be congruent if the corresponding sides and angles of the two triangles are equal in measure. Thus, if the two triangles are superimposable, then they are congruent. For example, $\vartriangle AQC$ and $\vartriangle PQR$ are similar triangles, not congruent because they are not superimposed but they are in a certain ratio.

Here, we are given that $\vartriangle ABC \cong \vartriangle RPQ$.

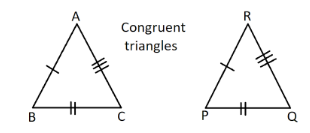
Therefore, by definition, we can conclude that by corresponding parts of congruent triangles, following sides are equal:
$ \Rightarrow AB = RP$
$ \Rightarrow BC = PQ$
$ \Rightarrow AC = RQ$
Now since $BC = PQ$ , $BC \ne QR$ as they are not corresponding sides of the given congruent triangles.

Hence, the given statement is false.

Note: 1) The order of the triangles is very important. If it had been given that $\vartriangle ABC \cong \vartriangle PQR$, then as per corresponding parts of congruent triangles (C.P.C.T.), the equal pair of sides would have been-
$ \Rightarrow AB = PQ$
$ \Rightarrow BC = QR$
$ \Rightarrow AC = PR$
In this case, the given statement asking whether $BC = QR$ would have been true.
Therefore, the order of the triangles must be observed properly.