Question

It is given that \[\angle XYZ = 64^\circ \]and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects \[\angle ZYP\], find reflex \[\angle QYP\]in degrees.

Answer 1

Hint: The sum of all angles of a straight line must be equal to \[180^\circ \] This is also called the supplementary angle . And if the bisector divides the straight line into 2 equal parts then the angles will also get divided into equal parts. And here we have to find the reflex angle which means that the angle must be greater than supplementary angle and less than complementary angle.

Complete step-by-step answer:
Here as we know XYP is a straight line.
Now let us first of all draw a diagram according to the question.

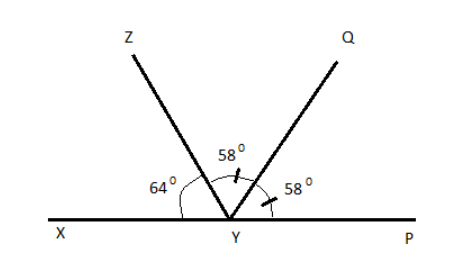
As we know that XYP is a straight line and \[\angle XYZ = 64^\circ \].
And we also know that a linear pair of angles is formed when two lines intersect.
So, according to linear pair property of straight line
\[ \Rightarrow \]\[\angle XYZ + \angle PYZ = 180^\circ \]
Now putting the given values and solving the above equation will give the value of the remaining angle.
\[ \Rightarrow \;64^\circ + \angle PYZ = 180^\circ \]
\[ \Rightarrow \angle PYZ = 180^\circ - 64^\circ = 116^\circ \]
So, from here we have \[\angle PYZ = 116^\circ \]and we know that YQ bisects \[\angle PYZ{\text{ }}({\text{ i}}{\text{.e}}{\text{. 116}}^\circ {\text{ )}}\]in two equal angles.
Now we can say that
\[ \Rightarrow \angle ZYQ = \angle QYP = \dfrac{{116^\circ }}{2}\]

So, \[\angle ZYQ = \angle QYP = 58^\circ \]

Note:
Whenever we come up with a type of problem we must use the concept of linear pair because this concept will give us the value of the remaining angle. And once we will get the value of the remaining angle we can use the concept of the bisector to get the value of the desired angle.