Question

It is given that $\angle XYZ = {64^ \circ }$ and $XY$ is produced to point $P$. Draw a figure from the given information. If ray $YQ$ bisects \[\angle ZYP\], find \[\angle XYQ\] and reflex \[\angle QYP\].

Answer 1

Hint:
For this type of geometrical problem we have to draw the figure first and then we will see what to find next. As we know the angle subtended by a straight line is ${180^ \circ }$. And if any line bisects the straight line in two half equal then the angles become also half. Using all these we can find the angle asked from us.

Complete step by step solution:
Since in the question it is given that we have a straight line and named it as $XYP$.
So by using the condition of linear pair, we can write the equation as
$ \Rightarrow \angle XYZ + \angle ZYP = {180^0}$
And from here we can calculate$\angle ZYP$, and it will be equal to
$ \Rightarrow \angle ZYP = {180^0} - \angle XYZ$
Putting the values, we get
$ \Rightarrow \angle ZYP = {180^0} - {64^ \circ }$
On solving we get
$ \Rightarrow \angle ZYP = {116^ \circ }$

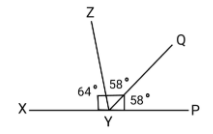
Now since $YQ$bisects $\angle ZYP$
Therefore, the equation will become
\[ \Rightarrow \angle ZYQ = \angle QYP = \dfrac{1}{2}\angle ZYP\]
And on substituting the values, we get
\[ \Rightarrow \angle ZYQ = \angle QYP = \dfrac{1}{2} \times {116^ \circ }\]
And so on solving, we get
\[ \Rightarrow \angle ZYQ = \angle QYP = {58^ \circ }\]
Since, \[\angle XYQ = \angle XYZ + \angle ZYQ\]
Therefore, on substituting the values, we get
\[ \Rightarrow \angle XYQ = {64^ \circ } + {58^ \circ }\]
And on solving it will become
\[\angle XYQ = {122^ \circ }\]
Now we have to find the reflex angle $\angle QYP$
So it will become
Reflex $\angle QYP = {360^ \circ } - \angle QYP$
On substituting the values, we get
Reflex $\angle QYP = {360^ \circ } - {58^ \circ }$
And on solving it, we get
Reflex $\angle QYP = {302^ \circ }$

Therefore, Reflex $\angle QYP = {302^ \circ }$and\[\angle XYQ = {122^ \circ }\].

Note:
For solving such types of problems our geometry should be strong and we should understand the logic of the equation rather than memorizing geometric equations. And the most important thing is the rough diagram based on the problem. As it helps to solve the problem very easily, as we can see in this question itself. So we can say that we should keep our fundamental geometry clear to solve such problems.