Question

Is it true that for a value of $n$ (n-principal quantum number), the value of ${m_l}$ (${m_l}$-magnetic quantum number) is equal to ${n^2}$ ? If it is true, can you please explain this to me? Thanks.

Answer 1

Hint: In the atom, there are four quantum numbers which are: Principal quantum number ($n$), Azimuthal quantum number ($l$ ), magnetic quantum number (${m_l}$ ) and spin quantum number (${m_s}$ ). Each electron of the atom has its own unique set of quantum numbers.

Complete answer:
For this we have to know about the four quantum numbers. Principal quantum number ($n$), is to describe the principal electron shell, i.e. the shell in which the electron is present. Azimuthal quantum number ($l$ ), describes the shape of the orbital in which an electron is present. Magnetic quantum number (${m_l}$ ) is to determine the number of orbitals and their orientation within the shell. And the spin quantum number (${m_s}$ ) tells the direction of the electron spin.
The Azimuthal quantum number $l$ depends upon the value of principal quantum $n$ whereas ${m_l}$ values depend upon Azimuthal quantum number $l$.
The Azimuthal quantum number $l$ can be any value ranging from $0$ to $n - 1$ when the principal quantum number $n$ is $n$. So, the Azimuthal quantum number $l$:
$l = 0,1,2,......,(n - 1)$
The range of magnetic quantum number ${m_l}$ from $ - l$ to $l$ . So, the magnetic quantum number ${m_l}$:
${m_l} = \; - l,...., - 1,0,1,...,l$
If we substitute the value of $l$, we can get the relation between ${m_l}$ and $n$ which can be:
${m_l} = \; - (n - 1),..., - 1,0,1,...,(n - 1)$
To make it more clear let’s take an example $n = 2$ ,
for $l = 0$ , ${m_l} = 0$
And for $l = 1$, ${m_l} = \{ - 1,0,1\} $
We can see that the values of ${m_l}$ is not even close to ${n^2}$but the total number of ${m_l}$ is, if you take the values of $l$, is indeed equal to ${n^2}$.
The magnetic quantum number tells us about the number of orbitals the subshell has. By above example, we can see if $n = 2$ then $l = 0$ , ${m_l} = 0$ indicates $2s - orbital$

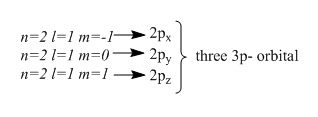
This indicates the second energy level has two subshells , one is of $2s$ and other one is $2p$ subshell. And by ${m_l}$ values we can get the number of orbitals each subshell has. For $2s - subshell$, there is only one possible value of ${m_l}$ so it has one orbital. Whereas $2p - subshell$ there are three orbitals as it has three different values of ${m_l}$. Hence the total number of orbitals in the second energy level is $4$ , which equals ${n^2}$ .

Note:
The only one quantum number which is not dependent on the other is spin quantum number as it indicates the direction of the electron spin. The spin of $ + \dfrac{1}{2}$ is represented by $ \uparrow $ , whereas the spin $ - \dfrac{1}{2}$ is represented by $ \downarrow $ .