Question

Is it possible to construct quadrilateral ABCD in which \[AB = 3\,cm\] , \[BC = 4\,cm\] , \[CD = 5.4\,cm\] , \[DA = 5.9\,cm\] and diagonal \[AC = 8\,cm\] ?. If not, why?

Answer 1

Hint: Here in this question belongs to construction topic, given the length of four sides and one diagonal of quadrilateral we have to try to construct the possible quadrilateral of given measurements by using a geometrical instruments like centimeter scale, compass with provision of fitting a pencil, this can also be check by using a triangle inequality i.e., sum of two sides is always greater than the third side.

Complete step by step solution:
Consider the given question:
Given, the length of four sides and one diagonal of quadrilateral ABCD i.e.,
 \[AB = 3\,cm\] , \[BC = 4\,cm\] , \[CD = 5.4\,cm\] , \[DA = 5.9\,cm\] and diagonal \[AC = 8\,cm\]
To construct the possible quadrilateral ABCD follow the below steps:
Steps of Construction:
First, by using a side-side-side (S-S-S) construction, draw a triangle \[\Delta \,\,ACD\] . Draw a length of diagonal line \[AC = 8\,cm\] .

Now, by using a compass, take a length or radius of \[5.9\,cm\] and draw an arc by taking A as centre. Do the same by taking C as centre and length of \[5.4\,cm\] . Then join the arc intersection point to A and C and label it as D.

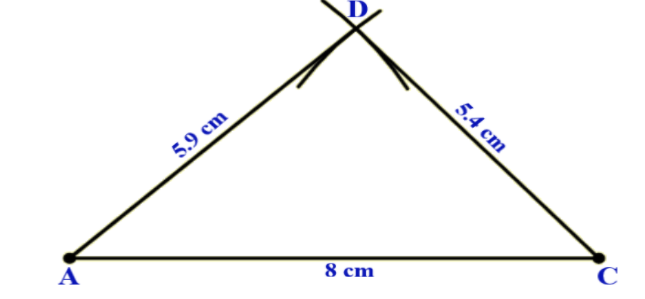
Now for remaining vertex B, using a compass take a length of \[3\,cm\] and draw an arc by taking A as centre. Do the same by taking C as the centre and length of \[4\,cm\] .

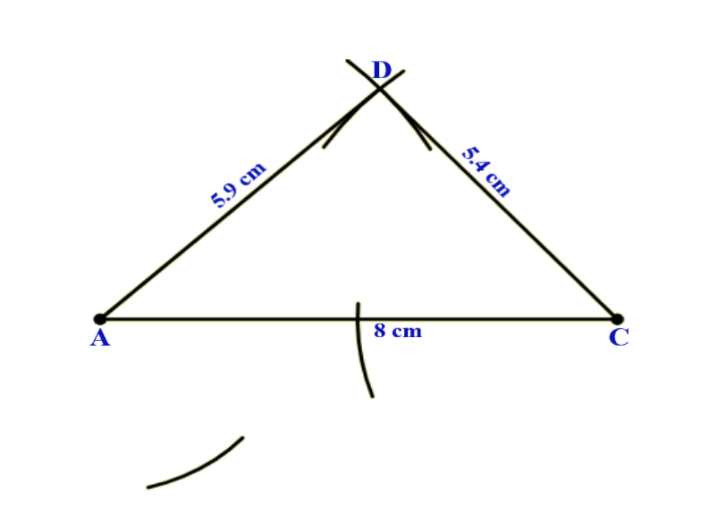
Here, the drawn arcs from A and C towards point B are not intersecting then it is not possible to construct a quadrilateral ABCD.
As we know the quadrilateral having a diagonal gives a two-triangles i.e., In quadrilateral ABCD, line AC be the diagonal it gives a two-triangles \[\Delta \,\,ACD\] and \[\Delta \,\,ABD\] .
In \[\Delta \,\,ABD\] ,
 \[AB + BC = 3 + 4 = 7cm\] and \[AC = 8cm\]
Here, the sum of two sides of a triangle is less than the third side.
It is not satisfied a triangle inequality
Hence, not possible to draw a \[\Delta \,\,ABD\] , then
Construction of a quadrilateral ABCD is also not possible.

Note: When doing construction handling the instruments carefully, the S-S-S construction means draw a triangle using a length of three sides; it's a one of the axioms or criterion of triangles. There are always two triangles within the quadrilateral having one diagonal and those triangles should satisfy the triangle inequality.