Question

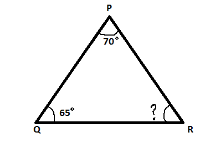
In\[\vartriangle PQR,\angle P = {70^ \circ },\angle Q = {65^ \circ }\] then find $\angle R$?

Answer 1

Hint: We solve for the angle by substituting the given angles in the property of sum of interior angles of a triangle. Add the values of given angles and subtract from total sum of angles.
* Sum of interior angles of a triangle is $ = {180^ \circ }$

Complete step-by-step answer:
We have a triangle whose two angles are given and we have to find the third angle.
In\[\vartriangle PQR,\angle P = {70^ \circ },\angle Q = {65^ \circ }\]
We know from the property of sum of interior angles,
\[ \Rightarrow \angle P + \angle Q + \angle R = {180^ \circ }\]
Substitute the values of\[\angle P = {70^ \circ },\angle Q = {65^ \circ }\]in LHS of the equation.
$ \Rightarrow {70^ \circ } + {65^ \circ } + \angle R = {180^ \circ }$
Add the angles on LHS of the equation
$ \Rightarrow {135^ \circ } + \angle R = {180^ \circ }$
Shift all the constant values in degrees to one side of the equation.
$ \Rightarrow \angle R = {180^ \circ } - {135^ \circ }$
$ \Rightarrow \angle R = {45^ \circ }$

Therefore $\angle R = {45^ \circ }$

Note: Many times we will be given the measure of one angle and we have to find the other two angles, in these kinds of questions look if the triangle is given to be isosceles (having two angles equal ) or is given to be right angled ( one angle is right angle), then we can use the sum of interior angles property and find the remaining angles.
Students many times make mistakes when they don’t change the sign of the value while shifting the value from one side of the equation to another side of the equation. Keep in mind the sign changes from positive to negative and vice-versa when shifting a value from one side of the equation to the other side of the equation.