Question

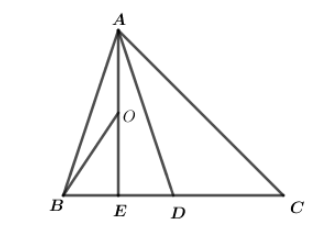
In$\vartriangle ABC$, it is given that D is the midpoint of BC, E is the midpoint of BD and O is the midpoint of AE. Then find the value of$ar\left( {\vartriangle BOE} \right)$.

Answer 1

Hint:Here, we will use the property of the median of a triangle that says “median of a triangle divides the triangle into two triangles of equal areas that is equal to half of the whole area of the triangle”. Apply median concept in triangles ABC, ABD and ABE, to relate the areas of these three triangles.

Complete step-by-step answer:
Given that, in$\vartriangle ABC$, D is the midpoint of side BC of$\vartriangle ABC$. Therefore AD is the median of $\vartriangle ABC.$
As we know that “median of a triangle divides the triangle into two triangles of equal areas that is equal to half of the whole area of the triangle”.
 $\therefore ar(\vartriangle ABD) = ar(\vartriangle ADC) = \dfrac{1}{2}ar(\vartriangle ABC)$
Now, E is the midpoint of side BD of$\vartriangle ABD$
So, AE is the median of $\vartriangle ABD$
$\therefore ar(\vartriangle ABE) = ar(\vartriangle AED) = \dfrac{1}{2}ar(\vartriangle ABD)$
Again, O is the midpoint of side AE, in $\vartriangle ABE$
So, BO is the median of $\vartriangle ABE$
Comparing areas of triangles, we get
$\therefore ar(\vartriangle BOE) = ar(\vartriangle BOA) = \dfrac{1}{2}ar(\vartriangle ABE)$
$\therefore ar(\vartriangle BOE) = \dfrac{1}{2}ar(\vartriangle ABE)$
$ \Rightarrow ar(\vartriangle BOE) = \dfrac{1}{4}ar(\vartriangle ABD)$ $\left\{ {\because ar(\vartriangle ABE) = \dfrac{1}{2}ar(\vartriangle ABD)} \right\}$
$ \Rightarrow ar(\vartriangle BOE) = \dfrac{1}{8}ar(\vartriangle ABC)$ $\left\{ {\because ar(\vartriangle ABD) = \dfrac{1}{2}ar(\vartriangle ABC)} \right\}$

Note:These types of questions are purely based on geometrical concepts, which can be solved using geometrical theorems and definitions. In a triangle the line joining the midpoint of a side to its opposite vertex is called the median of the triangle. There are 3 medians of a triangle. These three medians meet at a point that is called the centroid of the triangle. It is denoted by G. The centroid divides the median in the ratio 2:1. The centroid always lies inside a triangle. Median bisects the triangle into two triangles of equal area and the area of each triangle is half of the given triangle. Medians of equilateral triangles are equal. Two medians on the equal sides of a isosceles triangle are equal.