Question

Into a circular drum of radius $ 4.2m $ and height $ 3.5m $ , how many full bags of wheat can be emptied if the space required for wheat in each bag is $ 2.1{m^3}? $ (take $ \pi = 3.14 $ )

Answer 1

Hint: Since from the given that circular drum as the radius of $ 4.2m $ which is half the diameter $ d = \dfrac{r}{2} $ (so the total diameter of the drum is $ 8.4m $ ) and also the height is given as $ 3.5m $ for the circular drum, pie value can be written as $ \pi = 3.14 $ .We are asked how many find full bags of wheat can be emptied. The required space for the given wheat is $ 2.1{m^3} $ in each bag.
The formula used: $ \pi {(r)^2}h $ (volume of the drum)

Complete step-by-step answer:
Since the volume of the drum is $ \pi {(\dfrac{d}{2})^2}h $ (half of the diameter is the radius) and thus the volume of the drum is $ \pi {(r)^2}h $ ; now substitute the know values into the formula we get $ \pi {(r)^2}h \Rightarrow 3.14 \times {(4.2)^2} \times 3.5 $

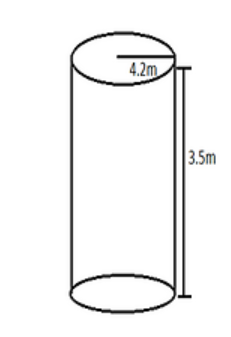
(Height is three point five, the radius is four-point two also the value of pie is three point one four)
Since the volume of each bag of the wheat is given as $ 2.1{m^3} $ ; to find the number of bags that we need to fit into that space required of the given circular drum will be found by dividing into the volume of bags;
Hence the number of bags $ \Rightarrow \dfrac{{3.14 \times {{(4.2)}^2} \times 3.5}}{{2.1}} $ (square can be written as the times of twice itself multiplication).
Thus, further solving we get the number of bags $ \Rightarrow \dfrac{{3.14 \times 4.2 \times 4.2 \times 3.5}}{{2.1}} = \dfrac{{193.86}}{{2.1}} $ (by use of multiplication)
Hence the number of bags that required is $ \Rightarrow \dfrac{{193.86}}{{2.1}} = 92.31 $ (by the use of division)
approximately $ 92 $ (after decimal less than $ 0.4 = 1 $ are $ 0.5 = 1 $ to be considered) bags that we will need to fill that circular drum

Note: Since the height and radius of the problem are given so that the required answer is the number of bags, if the number of bags and height is given, we are also able to apply the same formula and methods to find the radius of the problem. Since $ \pi = 3.14 $ is an irrational number because it was not in the $ \dfrac{p}{q} $ format.
Radius is half of the given diameter.