Question

How do you integrate \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} \] trigonometric substitution?

Answer 1

Hint: The given question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. We need to know the basic trigonometric formulae and conditions to make an easy calculation. Also, we need to know the basic integration formulae with the involvement of trigonometric components. We need to know how to perform integral functions.

Complete step by step solution:
The given expression is shown below,
 \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx = ? \to \left( 1 \right)\]
Let’s take \[x = 2\tan u\]
So, we get \[dx = 2{\sec ^2}udu\]
Let’s substitute these values in the equation \[\left( 1 \right)\] , we get
 \[
  \int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx = \int {\dfrac{{2{{\sec }^2}udu}}{{{{\left( {2\tan u} \right)}^2}\sqrt {4 + {{\left( {2\tan u} \right)}^2}} }}} \\
  \int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx \\
= \int {\dfrac{{2{{\sec }^2}udu}}{{4{{\tan }^2}u\sqrt {4 + 4{{\tan }^2}u} }}} \\
= \int {\dfrac{{2{{\sec }^2}udu}}{{2 \times 4{{\tan }^2}u\sqrt {1 + {{\tan }^2}u} }}} \\
= \int {\dfrac{{{{\sec }^2}udu}}{{4{{\tan }^2}u\sqrt {1 + {{\tan }^2}u} }}} \;
 \]
So, we get
 \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx \\
= \dfrac{1}{4}\int {\dfrac{{{{\sec }^2}udu}}{{{{\tan }^2}u\sqrt {1 + {{\tan }^2}u} }}} \to \left( 2 \right)\]
We know that,
 \[
  {\tan ^2}u = \dfrac{{{{\sin }^2}u}}{{{{\cos }^2}u}} \\
  \sqrt {1 + {{\tan }^2}u} = \sqrt {1 + \dfrac{{{{\sin }^2}u}}{{{{\cos }^2}u}}} \\
= \sqrt {\dfrac{{{{\cos }^2}u + {{\sin }^2}u}}{{{{\cos }^2}u}}} \;
 \]
We know that \[{\sin ^2}u + {\cos ^2}u = 1\]
So, we get
 \[\sqrt {1 + {{\tan }^2}u} = \sqrt {\dfrac{{{{\cos }^2}u + {{\sin }^2}u}}{{{{\cos }^2}u}}}
= \sqrt {\dfrac{1}{{{{\cos }^2}u}}}
= \sqrt {{{\sec }^2}u} = \sec u\]
[ We know that \[\dfrac{1}{{\cos \theta }} = \sec \theta \] ]
So, the equation \[\left( 2 \right)\] becomes,
 \[\left( 2 \right) \to \int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx
= \dfrac{1}{4}\int {\dfrac{{{{\sec }^2}udu}}{{{{\tan }^2}u\sqrt {1 + {{\tan }^2}u} }}} \]
 \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx \\
= \dfrac{1}{4}\int {\dfrac{{{{\sec }^2}udu}}{{{{\tan }^2}u \cdot \sec u}}} = \dfrac{1}{4}\int {\dfrac{{\sec udu}}{{{{\tan }^2}u}}} \]
We know that \[\sec u = \dfrac{1}{{\cos u}}\] and \[\dfrac{1}{{{{\tan }^2}u}}= \dfrac{{{{\cos }^2}u}}{{{{\sin }^2}u}}\] .
So, the above equation can be written as,
 \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx
= \dfrac{1}{4}\int {\dfrac{{\sec udu}}{{{{\tan }^2}u}}} \\
= \dfrac{1}{4}\int {\dfrac{1}{{\cos u}}} \cdot \dfrac{{{{\cos }^2}u}}{{{{\sin }^2}u}}du \\
= \dfrac{1}{4}\int {\dfrac{{\cos u}}{{{{\sin }^2}u}}du} \]
 \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx = \dfrac{1}{4}\int {\dfrac{{\cos u}}{{{{\sin }^2}u}}du} \] \[ \to \left( 3 \right)\]
Let’s take \[v = \sin u\]
So, we get \[dv = \cos udu\]
So, the equation \[\left( 3 \right)\] becomes,
 \[\left( 3 \right) \to \int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx = \dfrac{1}{4}\int {\dfrac{{\cos u}}{{{{\sin }^2}u}}du} \]
 \[I = \dfrac{1}{4}\int {\dfrac{1}{{{v^2}}}} dv\]
The above equation can also be written as,
 \[I = \dfrac{1}{4}\int {{v^{ - 2}}} dv\]
We know that,
 \[\int {{x^n}} = \dfrac{{{x^{n + 1}}}}{{n + 1}}\]
So, we get
 \[I = \dfrac{1}{4}\left( {\dfrac{{{v^{ - 2 + 1}}}}{{ - 2 + 1}}} \right) + c = \dfrac{1}{4} \times \dfrac{{ - 1}}{v} + c\]
We know that \[v = \sin u\]
So, we get
 \[I = \dfrac{{ - 1}}{{4\sin u}} + c\] \[ \to \left( 4 \right)\]
We know that
 \[x = 2\tan u\]
The above equation can also be written as,
 \[\tan u = \dfrac{x}{2}\]
 \[\tan u = \dfrac{{opposite}}{{adjacant}}\]

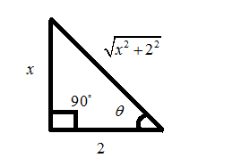
So, we get
 \[\sin u = \dfrac{{opposite}}{{hypotenuse}} = \dfrac{x}{{\sqrt {{x^2} + {2^2}} }} = \dfrac{x}{{\sqrt {{x^2} + 4} }}\]
By using these value the equation \[\left( 4 \right)\] becomes,
 \[\left( 4 \right) \to I = \dfrac{{ - 1}}{{4\sin u}} + c\]
 \[I = \dfrac{{ - 1}}{{4\left( {\dfrac{x}{{\sqrt {{x^2} + 4} }}} \right)}} + c\]
The above equation can also be written as,
 \[I = \dfrac{{ - \sqrt {{x^2} + 4} }}{{4x}} + c\]
So, the final answer is,
 \[\int {\dfrac{1}{{{x^2}\sqrt {4 + {x^2}} }}} dx = \dfrac{{ - \sqrt {{x^2} + 4} }}{{4x}} + c\]
So, the correct answer is “$\dfrac{{ - \sqrt {{x^2} + 4} }}{{4x}} + c$”.

Note: To solve these types of questions we would remember the basic trigonometric formula and conditions. Note that if a constant term is present inside the integral functions, we can take the constant term to the outside of the integral. Also, note that \[\sin \theta \] is defined as the opposite side value divided by hypotenuse side value in the rectangular triangle, \[\cos \theta \] is defined as the adjacent side value divided by hypotenuse side value in the rectangular triangle, and \[\tan \theta \] is defined as the opposite side value divided by the adjacent side value in a rectangular triangle.