Question

Integral \[\int\limits_{0}^{1}{\left| \sin \left( 2\pi x \right) \right|dx}\] is equal to
A. 0,
B. \[-\dfrac{1}{\pi }\],
C. \[\dfrac{1}{\pi }\],
D. \[\dfrac{2}{\pi }\].

Answer 1

Hint: We start solving the problem by taking \[2\pi x=t\] and converting $dx$ in terms of $dt$. We then substitute the obtained results and use the properties of modulus functions in place of integrand to proceed through the problem. We then use the results $\int{\sin xdx=-\cos x+C}$, $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)dx=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)}$ and make necessary calculations to get the required result.

Complete step by step answer:
As mentioned in the question, we have to find the value of the definite integral \[\int\limits_{0}^{1}{\left| \sin \left( 2\pi x \right) \right|dx}\].
Now, first we will substitute the integrand as follows
\[2\pi x=t\].
Differentiating on both sides, we get.
\[d\left( 2\pi x \right)=dt\].
\[\Rightarrow 2\pi dx=dt\].
\[\Rightarrow dx=\dfrac{dt}{2\pi }\].
Now, on doing these changes, the integral transforms into the following \[\int\limits_{0}^{2\pi }{\left| \sin \left( t \right) \right|\dfrac{dt}{2\pi }}\].
We know the property of modulus function as $\left| x \right|=\left\{ \begin{matrix}
   x\text{, if }x>0 \\
   0\text{, if }x=0 \\
   -x\text{, if }x<0 \\
\end{matrix} \right.$. We use this property for the integrand.
We know that the sine function becomes positive from 0 to \[\pi \] negative from \[\pi \] to \[2\pi \].
So, now, the value of this integral can be evaluated as follows
\[=\int\limits_{0}^{\pi }{\left| \sin \left( t \right) \right|\dfrac{dt}{2\pi }}+\int\limits_{\pi }^{2\pi }{\left| \sin \left( t \right) \right|\dfrac{dt}{2\pi }}\].
\[=\dfrac{1}{2\pi }\times \left( \int\limits_{0}^{\pi }{\sin tdt}+\int\limits_{\pi }^{2\pi }{\left( -\sin t \right)dt} \right)\].
\[=\dfrac{1}{2\pi }\times \left( \int\limits_{0}^{\pi }{\sin tdt}-\int\limits_{\pi }^{2\pi }{\sin tdt} \right)\] ---(1).
We know that $\int{\sin xdx=-\cos x+C}$ and $\int\limits_{a}^{b}{{{f}^{'}}\left( x \right)dx=\left[ f\left( x \right) \right]_{a}^{b}=f\left( b \right)-f\left( a \right)}$. We use this result in equation (1).
\[=\dfrac{1}{2\pi }\times \left( \left[ -\cos t \right]_{0}^{\pi }-\left[ -\cos t \right]_{\pi }^{2\pi } \right)\].
\[=\dfrac{1}{2\pi }\times \left( \left[ -\cos \pi -\left( -\cos 0 \right) \right]-\left[ -\cos 2\pi -\left( -\cos \pi \right) \right] \right)\].
\[=\dfrac{1}{2\pi }\times \left( \left[ -\left( -1 \right)-\left( -1 \right) \right]-\left[ -1-\left( -\left( -1 \right) \right) \right] \right)\].
\[=\dfrac{1}{2\pi }\times \left( \left[ 1+1 \right]-\left[ -1-1 \right] \right)\].
\[=\dfrac{1}{2\pi }\times \left( \left[ 2 \right]-\left[ -2 \right] \right)\].
\[=\dfrac{1}{2\pi }\times \left( 4 \right)\].
\[=\dfrac{2}{\pi }\].
∴ The value of \[\int\limits_{0}^{1}{\left| \sin \left( 2\pi x \right) \right|dx}\] is \[\dfrac{2}{\pi }\].

So, the correct answer is “Option D”.

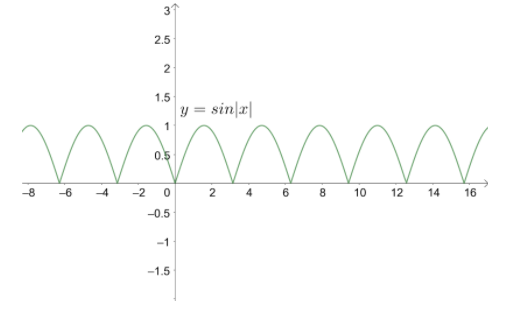
Note: We can also solve the problem by using the property of the periodic function. From the graph of $\left| \sin x \right|$, we can see that the repetition in the values of y in the curve. So, we can take limits from 0 to $\pi $ for getting the result. We know that for a periodic function f of period P with $n=kP$ is $\int\limits_{o}^{n}{f\left( x \right)dx=k\int\limits_{0}^{p}{f\left( x \right)dx}}$ to use for the integrand.