Question

Inside a triangular garden, there is a flower bed in the form of a similar triangle. Around the flowerbed runs a uniform path of such a width that the sides of the garden are double of the corresponding sides of the flower bed. The area of the paths and the flower beds are in the ratio-
A. 1 : 1
B. 1 : 2
C. 1 : 3
D. 3 : 1

Answer 1

Hint:In this problem, the concept of similar triangles will be applied. It has been given that the triangular flower bed inside the garden is similar to the triangular garden. We will use the property that the square of ratio of the sides of similar triangles is proportional to the ratio of their areas. This will give us the ratio of areas of the two triangles. We will use that to find the ratio of area of the paths and the flower beds.

Complete step-by-step answer:
We have been given that the garden has a triangular flower bed such that the two triangles are similar. So, we can draw their figure as-

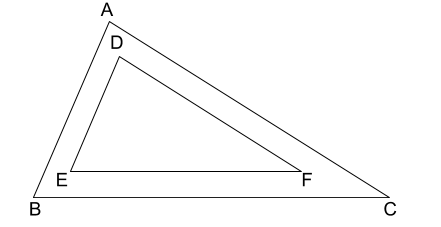
Let the triangle ABC represent the garden, and the triangle DEF represent the flower bed. It has been given that the two triangles are similar such that the length of the sides of the garden are double to that of the sides of the flower bed. We will now use the formula that the ratio of the areas of similar triangles are proportional to the square of the ratio of their sides.
 $ \dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle DEF} \right)}} = {\left( {\dfrac{{AB}}{{DE}}} \right)^2} = {\left( {\dfrac{{BC}}{{EF}}} \right)^2} = {\left( {\dfrac{{AC}}{{DF}}} \right)^2} $
We have been given that the sides of the garden are double, so the ratio is 2 : 1. Substituting these values we can write that-
 $ \dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle DEF} \right)}} = {\left( {\dfrac{2}{1}} \right)^2} = \dfrac{4}{1} $
But, we need to find the ratio of areas of the path and the flower bed. We know that-
 $ \begin{align}
  &ar\left( {\vartriangle ABC} \right) = ar\left( {\vartriangle DEF} \right) + ar\left( {path} \right) \\
  &\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle DEF} \right)}} = \dfrac{4}{1} = \dfrac{{ar\left( {\vartriangle DEF} \right) + ar\left( {path} \right)}}{{ar\left( {\vartriangle DEF} \right)}} \\
  &1 + \dfrac{{ar\left( {path} \right)}}{{ar\left( {\vartriangle DEF} \right)}} = \dfrac{4}{1} \\
  &\dfrac{{ar\left( {path} \right)}}{{ar\left( {\vartriangle DEF} \right)}} = 4 - 1 = \dfrac{3}{1} \\
\end{align} $

Hence, the required ratio is 3 : 1. The correct option is D.

Note: In such types of questions, the common mistake by students is that they usually find and mark the wrong ratio as the option. They usually find the ratio of areas of the outer and inner triangles, which is incorrect. Hence, we should always read the question carefully to correctly find the answer. The ratios of area of similar triangles are given by square of ratios of corresponding sides, not just ratios of sides,this is very important else we may end up getting wrong answers.