Question

Initially, the car A is 10.5 m ahead of the car B. Both start moving at time t=0 in the same direction along a straight line. The velocity-time graph of two cars is shown in the figure. The time when the car B will catch the car A, will be
A: 21 sec
B: $2\sqrt{5}$ sec
C: 20 sec
D: None of the above.

Answer 1

Hint: We’re given the one dimensional motion of two bodies. We can find the answer using the basic equations of motion, by substituting the given values in the formulas.
$s=ut+\dfrac{1}{2}a{{t}^{2}}$: The second equation of motion, where s is the total distance travelled by the body, u is the initial velocity, a is the acceleration of the body and t is the time taken to travel the distance.

Complete step by step answer:
We are given two cars A and B.
Car A is 10.5m ahead of car B.

Let us assume that car B crosses car A at point C, as per the diagram.
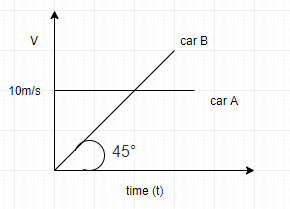
From graph, we can say that velocity of car A ${{V}_{A}}=10m/s$
If the time taken for car A to reach C is t seconds,

Distance $x=10t$
Considering Car B,
From graph, the acceleration of B is $\tan {{45}^{\circ }}=1$
Its initial velocity is zero
Hence ${{S}_{B}}=0+\dfrac{1}{2}a{{t}^{2}}=\dfrac{{{t}^{2}}}{2}$
Since A is 10.5m ahead of B,
$\begin{align}
  & 10.5+x={{S}_{B}}=\dfrac{{{t}^{2}}}{2} \\
 & \Rightarrow 21+2x={{t}^{2}} \\
\end{align}$
But we have proved that $x=10t$
Hence
 $\begin{align}
  & 21+2(10t)={{t}^{2}} \\
 & \Rightarrow 21+20t={{t}^{2}} \\
 & \Rightarrow {{t}^{2}}-20t-21=0 \\
\end{align}$
Therefore $t=\dfrac{20\pm \sqrt{400+84}}{2}=21s$
Hence, time taken for B to cross A is 21 seconds.

So, the correct answer is “Option A”.

Note:
Equations of motion elaborate the basic concepts of the motion of objects like position, velocity or the acceleration of an object at different times. These three equations of motion help to study the motion of an object in 1D, 2D and 3D.
First Equation of Motion : $v=u+at$, Second Equation of Motion : $s=ut+\dfrac{1}{2}a{{t}^{2}}$
Third Equation of Motion : ${{v}^{2}}={{u}^{2}}+2as$