Question

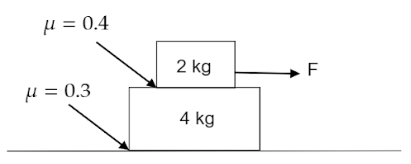
Initially system is at rest, as shown in figure;
(a) Find maximum value of $\left( 2 \right)$ for which no block will move.
(b) Find acceleration of block $\left( 1 \right)$ and $\left( 2 \right)$, friction force between block $\left( 1 \right)$ and $\left( 2 \right)$ as well as between
2 and ground surface if.
(i)$F = 4{\text{ }}N$ (ii) $F = 8{\text{ }}N$ (iii) $F = 16{\text{ }}N$

Answer 1

Hint: We will first consider the upper block and eventually by free body diagram we will find out the maximum force for which the block will not move. When the block does not move it means that the acceleration of the block is $0$. Furthermore, after that with the help of the values given in the diagram we can find the acceleration of each block with another or ground.

Complete step by step answer:

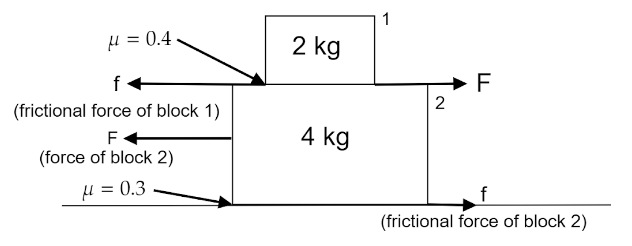
(a) From the free body diagram the net force working down by the body of mass $2{\text{ }}kg$ is,
$mg = 2 \times 10 = 20{\text{ }}N - - - - \left( 1 \right)$
The normal $N$ is the force that balances the downward force $mg$. We know that the coefficient of friction $\mu $ working between the block $\left( 1 \right)$ and $\left( 2 \right)$ is $0.4 - - - - \left( 2 \right)$
Now, we get to know,
Frictional force $f = \mu N$
$ \Rightarrow f = \mu mg$

Substituting $mg$ from equation $\left( 1 \right)$ and $\mu $ from $\left( 2 \right)$
$f = 20 \times 0.4 \\
\Rightarrow f = 8{\text{ }}N - - - \left( 3 \right) \\ $
Now, from the free body diagram,
$F - f = ma - - - - \left( 4 \right)$
According to the question the body does not move means the acceleration $\left( a \right)$ is $0$.
Here, mass $\left( m \right) = 2{\text{ }}kg$
Putting $m$ and $a$ in equation $\left( 4 \right)$ and the value of $f$ from equation $\left( 3 \right)$ we get,
$F - 8 \geqslant 0 \\
\Rightarrow F \geqslant 8{\text{ }}N $
So, the max force till which the body does not move is $8{\text{ }}N$.

(b) According to the question the acceleration of block $\left( 1 \right)$ is,
$F - f = ma$ where $m = 2{\text{ }}kg$ and $f = \mu mg = 0.4 \times 2 \times 10 = 8{\text{ }}N$
Thus acceleration is,
$a = \dfrac{{F - 8}}{m} - - - - \left( 5 \right)$
$ \Rightarrow a = \dfrac{{F - 8}}{2}$
When (i)$F = 4{\text{ }}N$then $a = - 4{\text{ }}\dfrac{m}{{{s^2}}}$ (negative sign implies retardation)
When (ii) $F = 8{\text{ }}N$ then $a = 0{\text{ }}\dfrac{m}{{{s^2}}}$
When (iii) $F = 16{\text{ }}N$ then $a = 4{\text{ }}\dfrac{m}{{{s^2}}}$
Similarly, the acceleration of block $\left( 2 \right)$ is,
$F - f = ma$ where $f = 0.3 \times \left( {4 + 2} \right) \times 10 = 18{\text{ }}N$ and $m = \left( {2 + 4} \right) = 6{\text{ }}kg$

Thus acceleration is,
$a = \dfrac{{F - f}}{6} - - - - \left( 6 \right)$
When (i) $F = 4{\text{ }}N$then $a = - \dfrac{7}{3}{\text{ }}\dfrac{m}{{{s^2}}}$ (negative sign implies retardation)
When (ii) $F = 8{\text{ }}N$ then $a = - \dfrac{5}{3}{\text{ }}\dfrac{m}{{{s^2}}}$ (negative sign implies retardation)
When (iii) $F = 16{\text{ }}N$ then $a = - \dfrac{1}{3}{\text{ }}\dfrac{m}{{{s^2}}}$ (negative sign implies retardation)
Now, the frictional force $f$ only depends upon coefficient of friction $\mu $ and normal reaction $N$
For block $\left( 1 \right)$ and $\left( 2 \right)$ the frictional force $f$ is,
$f = \mu mg = 0.4 \times 2 \times 10 = 8{\text{ }}N$
For block $\left( 2 \right)$ and ground the frictional force $f$ is,
$\therefore f = 0.3 \times \left( {4 + 2} \right) \times 10 = 18{\text{ }}N$

Note: We must always draw a free body diagram for such a question. Frictional force always restricts the movement of a body. So, it is in the opposite direction of the main force. Moreover normal $N = mg$ and frictional force is $f = \mu mg$.