Question

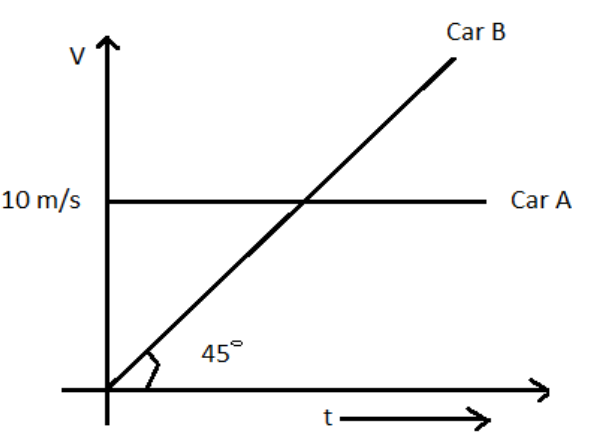
Initially car A is $10.5m$ ahead of car B. Both start moving at time $t = 0$ in the same direction along a straight line. The velocity time graph of two cars shown in figure. The time when the car B will catch the car A, will be:

A. $t = 21\sec $
B. $t = 2\sqrt 5 \sec $
C. $20\sec $
D. None of these

Answer 1

Hint: We know that equations of motion are equations that are helpful in determination of dynamic variables and behaviour of motion of a system. This problem is solved with the help of equation $s = ut + \dfrac{1}{2}at$ which gives the distance covered by any object. Here $s = $ distance covered, $a = $ acceleration, $u = $ initial velocity and $t = $ time. We can draw graphs of motions with the help of these equations.

Complete answer:
We have studied that the slope of velocity- time graph gives acceleration. We should also take care of the direction of acceleration. Here the given graph is velocity- time graph. Here the given graph is velocity- time graph. Hence the acceleration of Car a and B can be calculated with the help of a given graph. Acceleration of Car A $ = 0m/{s^2}$and acceleration of Car B $ = 1m/{s^2}$.Now distance covered by car A and B can be calculated with help of equation $s = ut + \dfrac{1}{2}at$. Hence;
If the distance covered by car A and car B are ${s_A}$ and ${s_B}$ respectively and it is given in the graph that initial velocity is $u = 10m/s$.

$
  {s_A} = ut + \dfrac{1}{2}a{t^2} \\
  {s_A} = 10 \times t + \dfrac{1}{2} \times 0 \times {t^2} \\
  {s_A} = 10t \\
 $

$
  {s_B} = ut + \dfrac{1}{2}a{t^2} \\
  {s_B} = 0 \times t + \dfrac{1}{2} \times 1 \times {t^2} \\
  {s_B} = \dfrac{{{t^2}}}{2} \\
 $

It is given in the problem statement that initially car A is $10.5m$ ahead of car B so ${s_B} - {s_A} = 10.5$. Now we will put the value of distances covered by car A and car B in the equation. We will get
$\dfrac{{{t^2}}}{2} - 10t = 10.5$
${t^2} - 20t - 21 = 0$
$t = 21\sec , - 1\sec $
As we know that time cannot be negative, so t = 21. The time when car B will catch car A is $t = 21\sec $.

So, the correct answer is “Option A”.

Note:
We have solved this question with the help of the equation of motion. Some important points were given in the problem statement which help in finding the time when the car B will catch the car A. We know that acceleration is a vector quantity so we should always be aware of the direction of the acceleration.