Question

Infinite rods of uniform mass density and length \[{\text{L, }}\dfrac{{\text{L}}}{2},{\text{ }}\dfrac{{\text{L}}}{4}......\]are placed one upon another up to infinite as shown in the figure. Find the x-coordinate of the center of mass.

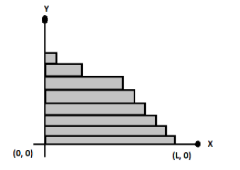
$A.{\text{ 0}}$
\[B.{\text{ }}\dfrac{{\text{L}}}{3}\]
\[C.{\text{ }}\dfrac{{\text{L}}}{2}\]
\[D.{\text{ }}\dfrac{{{\text{2L}}}}{3}\]

Answer 1

Hint: The point at which the whole mass of the system is concentrated is defined as the center of mass of a particle. If we have the data of the masses and the coordinates of the particles of an n-particle system.

Formulas used:
The coordinates of the center of mass of this system can be expressed as:
-\[{{\text{X}}_{COM}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum {{m_i}} }}\]
-\[{Y_{COM}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum {{m_i}} }}\]

Complete step by step answer:
\[x\] coordinate of Centre of mass is given by
\[{{\text{X}}_{COM}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum {{m_i}} }}\]
The numerator is
\[\sum\limits_{i = 1}^n {{m_i}{x_i}} = m\dfrac{L}{2} + \dfrac{m}{2}\left( {\dfrac{L}{4}} \right) + ......\]

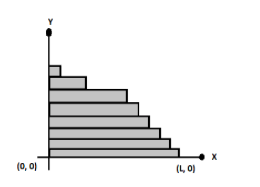
The denominator is,
\[\sum {{m_i}} = m + \dfrac{m}{2} + \dfrac{m}{4} + ......\]
So, \[{{\text{X}}_{COM}} = \dfrac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum {{m_i}} }} = \dfrac{{m\dfrac{L}{2} + \dfrac{m}{2}\left( {\dfrac{L}{4}} \right) + ......}}{{m + \dfrac{m}{2} + \dfrac{m}{4} + ......}}\]
\[{X_{COM}} = \dfrac{{mL\left( {\dfrac{1}{2} + \dfrac{1}{8} + \dfrac{1}{{32}} + ....} \right)}}{{m\left( {1 + \dfrac{1}{2} + \dfrac{1}{4} + ......} \right)}}\]
\[{X_{COM}} = \dfrac{{L\left( {\dfrac{{\dfrac{1}{2}}}{{1 - \dfrac{1}{4}}}} \right)}}{{\dfrac{1}{{\left( {1 - \dfrac{1}{2}} \right)}}}}\]
\[{X_{COM}} = \dfrac{{L\left( {\dfrac{4}{6}} \right)}}{2} = \dfrac{L}{3}\]

Hence, B option is correct

Additional information:
A large number of problems involving extended bodies or real bodies of finite size can be solved by taking them as Rigid Bodies. We define a rigid body as a body having a definite and unchanging shape.
Rigid body: It is a rigid assembly of particles with a fixed inter-particle distance.
Centre of mass for some bodies:
-A plane lamina - Point of intersection of diagonals
-Triangular plane lamina - Point of intersection of medians
-Rectangular or cubical block - Points of intersection of diagonals
-Hollow cylinder - Middle point of the axis of a cylinder

Note:
-The center of mass and center of gravity both are different.
-Centre of a mass of a body in which the total mass of the body is concentrated at one point.
-Where the center of gravity is the point at which the resultant of all gravitational forces on all the particles of the body acts.
-But for many objects, these two points are exactly in the same place when the gravitational field is uniform across the object.