Question

In$\Delta ABC$,$\angle C = 90^\circ $
If $BC = a,AC = b$and$AB = c$, find
(i)$c$when $a = 8cm$and $b = 6cm$
(ii) $a$when $c = 25cm$and $b = 7cm$
(iii) $b$when $c = 13cm$and $a = 5cm$

Answer 1

Hint: Take each of the above cases, then use Pythagoras theorem to find the missing value in that case. Repeat the same procedure to find the missing value in all the cases.

Complete step-by-step answer:

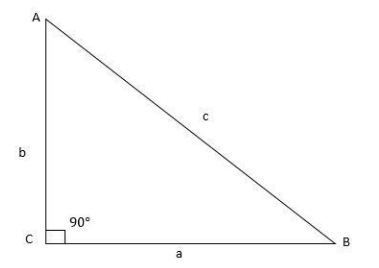
Using Pythagoras theorem,
Hypotenuse2=Perpendicular2+base2
(i) $c$when, $a = 8cm$and $b = 6cm$
Here,
$AC = b = 6cm$
$BC = a = 8cm$
$AB = c = ?$
Applying Pythagoras theorem,
$\Rightarrow A{B^2} = A{C^2} + B{C^2}$
$\Rightarrow {c^2} = {b^2} + {a^2}$
Putting the values,
$\Rightarrow {c^2} = {6^2} + {8^2}$
$\Rightarrow {c^2} = 64 + 36$
$\Rightarrow c = 10$

ii) Find $a$when $c = 25cm$ and $b = 7cm$
$AC = b = 7cm$
$BC = a = ?$
$AB = c = 25cm$
Applying Pythagoras theorem,
$\Rightarrow A{C^2} = A{B^2} + B{C^2}$
$\Rightarrow {c^2} = {b^2} + {a^2}$
$\Rightarrow {25^2} = {7^2} + {a^2}$
$\Rightarrow {a^2} = {25^2} - {7^2}$
$\Rightarrow {a^2} = 625 - 49$
$\Rightarrow {a^2} = 576$
$\Rightarrow a = 24$

(iii) $b$when $c = 13cm$and $a = 5cm$
Here,
$ AC = b = ?$
$ BC = a = 5cm$
$ AB = c = 13cm$
Applying Pythagoras theorem,
$\Rightarrow A{C^2} = A{B^2} + B{C^2}$
$\Rightarrow {c^2} = {b^2} + {a^2}$
$\Rightarrow {13^2} = {b^2} + {5^2}$
$\Rightarrow {b^2} = 169 - 25$
$\Rightarrow {b^2} = \sqrt {144} $
$\Rightarrow b = 12$

Note: A triangle having 90 Degree is a right angled triangle. The Pythagoras theorem is useful to calculate the values asked to find in a question.