Question

In Young’s experiment $\beta $ and $\beta '$ denotes distance between the two consecutive bright and dark fringes respectively, then
A). $\beta < \beta '$
B). $\beta > \beta '$
C). $\beta = \beta '$
D). \[\beta = \dfrac{{\beta '}}{2}\]

Answer 1

Hint: For solving this question first we will know the young’s experiment and then what is dark and bright fringes then finally the relation between these fringes and then the distance between the asked question, finally we will come to given options.

Formula used- The position of nth fringe is given by
${x_n} = \dfrac{{n\lambda D}}{d}$
Where
 \[n = 0,{\text{ }} \pm 1,{\text{ }} \pm 2 \ldots \]
For positive values of n we get bright fringes and for negative values of n we get dark fringes.
$\lambda $ is the wavelength
$D$ is the distance between the slits
$d$ is the distance between the sources.

Complete step-by-step answer:
Double slit experiment shows us that the light and matter both can display characteristics of classically defined waves and particles by the interference phenomena.

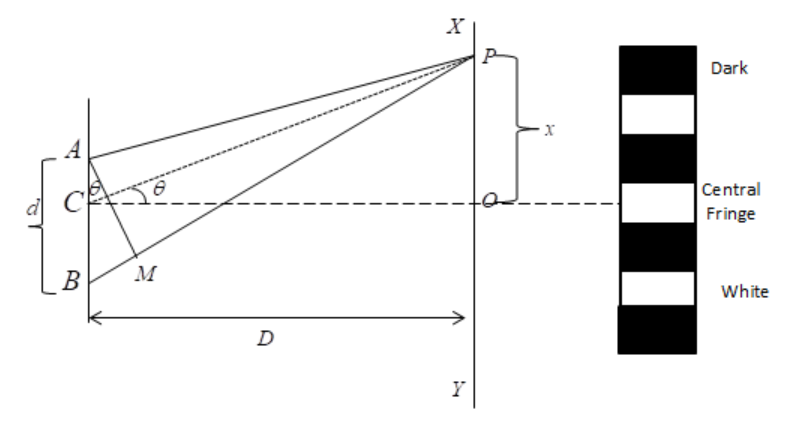
When the two or more waves are in phase causing a resultant wave of higher amplitude then it is called constructive interference and it form bright fringes
When two or more waves are out of phase then the resultant wave will have decreased in amplitude this is called destructive interference and it forms dark fringes.
Band width-The distance between any two consecutive bright or dark bands is called bandwidth.
Distance between $\left( {n + 1} \right)^{th}$ and $n^{th}$ order consecutive bright fringes from O is given by,
\[x(n + 1)-xn = \;\left[ {\left( {\dfrac{D}{d}} \right)} \right[\left( {n + 1} \right)\lambda \left] {{\text{ }}-\;\left( {\dfrac{D}{d}} \right)\left[ {\left( n \right)\lambda } \right]} \right] = \left( {\dfrac{D}{d}} \right)\lambda \]
Bandwidth,
\[\beta = \left( {\dfrac{D}{d}} \right)\lambda \]
The difference between two consecutive dark bands also equals \[\left( {D/d} \right)\beta \] . Although the bright and dark fringes have the same width, they are evenly spaced from each side.
Hence the correct option is “C”.

Note- The interference pattern, in which locations of maximum and minimum light intensity remain constant over time, is called a continuous or permanent interference pattern. The conditions for continuous interference formation can be laid down as:
(a) Both the sources should be coherent
(b) Both the sources should be very narrow
(c) Sources should lie very close to each other in order to form distinct and wide fringes.