Question

In Young's double-slit experiment, let \[A\] and \[B\] be the two slits. A thin film of thickness \[t\] and refractive index \[\mu \] is placed in front of\[A\] . Let \[\beta = \] the fringe width. Then the central maxima will shift
$A.$ Towards \[A\]
$B.$ Toward \[B\]
$C.$ By \[{\text{t}}\left( {\mu - 1} \right)\dfrac{\beta }{\lambda }\]
$D.$ By \[\mu {\text{t}}\dfrac{\beta }{\lambda }\]

Answer 1

Hint: A clear diagram has to be drawn for the double slit experiment in which a thin film is inserted. The formula of path difference has to be calculated in terms of the thickness of the slit and refractive index of the medium.
The formula of path difference in terms of fringe width also has to be included and then compared with the previous formula to find the amount of shift of the central maxima.

Formula Used:
The path difference,
\[{\Delta _{\text{o}}} = t(\mu - 1)\]
Where,
refractive index \[\mu \] and the thickness of the film is \[t\].
The path difference \[ = \dfrac{{{O_{central}}\lambda }}{\beta }\]
\[A\] and \[B\] are two slits separated by distance \[\lambda \] ,
\[\beta = \] the fringe width.

Complete step by step answer:
The data given the question is,
A and B are two slits
A thin film is placed in front of A having the thickness t and refractive index μ.
We have to find where the central maxima will shift.

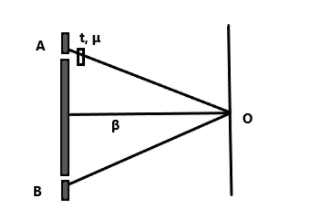
In the above figure, \[A\] and \[B\] are two slits separated by distance \[\lambda \], and a thin film of refractive index \[\mu \] and thickness \[t\] is placed at the slit \[A\].
After placing the thin film in front of slit A, the speed of light is less hence the light will be deleted. Where the light from B will be ahead in the path to light from \[A\] .
So, the path difference can be given by:
\[{\Delta _{\text{o}}} = t(\mu - 1)\]
The path difference at some point O on the screen \[ = \dfrac{{{O_{central}}\lambda }}{\beta }\]
So, \[\dfrac{{{O_{central}}\lambda }}{\beta } = t(\mu - 1)\]
\[{O_{central}} = \dfrac{{\beta t(\mu - 1)}}{\lambda }\](\[\beta = \] the fringe width).

Hence, the right answer is in option (C).

Note:
The optical path difference introduced due to the travel of a wave light in a denser medium is given as \[t\mu \] and the difference between two slits is \[t(\mu - 1)\].
Central maxima: In a single slit diffraction pattern, the point where secondary waves reinforce each other, resulting in the maximum intensity at that point, is called the central maximum.
To obtain constructive interference for a double slit,
\[d\sin \theta = m\lambda {\text{ for }}m = 0,1,2,3.....\]
To obtain destructive interference for a double slit,
\[d\sin \theta = \left( {m + \dfrac{1}{2}} \right)\lambda {\text{ for }}m = 0,1, - 1,2, - 2.....\]\[\]