Question

In which region is the acceleration decreasing?

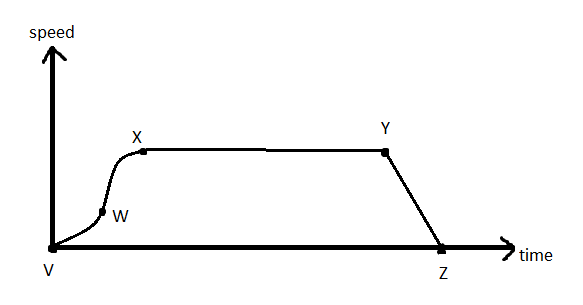
A. V to W
B. W to X
C. X to Y
D. Y to Z

Answer 1

Hint: Instantaneous acceleration is the slope of the tangent of a point on the speed-time graph. For decreasing acceleration in a region, the slope must keep on decreasing in that region.

Complete step by step answer:
The instantaneous acceleration of a body is the slope of the tangent of a point on the speed-time graph. In the regions where the slope is increasing, the acceleration of the body is also increasing. In the regions, where the slope is decreasing, the acceleration of the body keeps on decreasing.
For the region V to W, the slope of the tangent is increasing, so the acceleration is also increasing.
For the region W to X, the slope of the tangent is decreasing, so the acceleration is also decreasing.
For the region X to Y, the slope of the tangent remains zero, so the acceleration remains zero and does not change.
For the region Y to Z, the slope of the tangent remains constant and does not change. So the acceleration also remains constant and does not change.
Therefore, since only in the region W to X, the slope of the tangent is decreasing, so the acceleration is decreasing in that region.
So, the correct answer is B) W to X.

Note: Students may have a hard time in this question and may not be able to visualize the concept of the change in slope of the tangent. Thus, they may be tempted to mark the region Y to Z as the correct answer as they may think that the slope is negative there.
However, they must be careful and determine what they need to consider, a negative slope of the tangent or a negatively changing (reducing) slope of the tangent.
If instead of graphs a function is given, then they may apply the derivatives of the functions and evaluate their value for a point, which is easy to do as it is to be done mathematically.
However, such graphical questions are purposely given as students easily get confused as they cannot get numerical values for the derivatives here. For this an easy way to remember is that:
A positively changing (increasing) slope of tangent gives rise to a convex graph (curving up graph), and
A negatively changing (decreasing) slope of tangent gives rise to a concave graph (curving down graph).