Question

In which of the following cases a unique triangle can be constructed?
[a] AB = 4cm, BC = 8cm, CA = 2cm
[b] $BC=5.2cm,\angle B=90{}^\circ ,\angle C=110{}^\circ $
[c] $XY=5cm,\angle X=45{}^\circ ,\angle Y=60{}^\circ $
[d] An isosceles triangle in which the length of the equal sides is 6.2cm.

Answer 1

Hint: A triangle with given parameters is unique if two triangles with similar parameters are congruent to each other. Using the basic congruence criteria like SSS, SAS, ASA, AAS, RHS, etc. determine in which of the cases the triangle drawn will be unique.

Complete step-by-step answer:
We check option wise which of the options are correct.
We will be drawing two triangles (One with the names of vertices as given and the other with vertex names as given added with a subscript). We check in which of the cases the triangles are congruent and in which cases the triangles may not be congruent. Hence we will determine in which of the cases the triangle if drawn, will be unique. Finally, we will use the fact that the sum of two sides of a triangle is greater than the third side to verify whether the triangle can be drawn or not and the sum of the angles of the triangle should be $180{}^\circ $.
Consider two triangles ABC and ${{A}_{1}}{{B}_{1}}{{C}_{1}}$

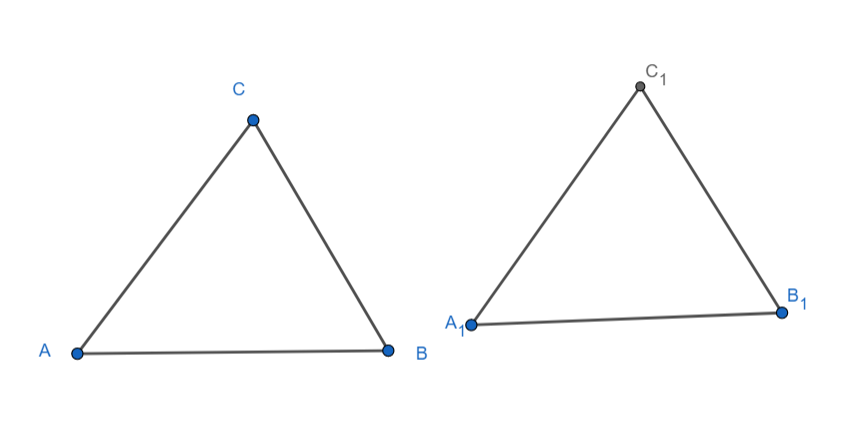
Let AB = 4cm, BC = 8cm, CA =2 cm.${{A}_{1}}{{B}_{1}}=4cm,{{B}_{1}}{{C}_{1}}=8cm,{{A}_{1}}{{C}_{1}}=2cm$
Hence in triangles $ABC$ and ${{A}_{1}}{{B}_{1}}{{C}_{1}}$, we have
$\begin{align}
  & AB={{A}_{1}}{{B}_{1}} \\
 & AC={{A}_{1}}{{C}_{1}} \\
 & BC={{B}_{1}}{{C}_{1}} \\
\end{align}$
Hence by SSS congruence criterion, we have $\Delta ABC\cong \Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}$
Hence if the triangle exists, it will be unique.
But, we have AB+AC = 4+2 = 6 < BC
Hence, it is not possible to construct a triangle with the given dimensions.
Consider two triangles ABC and ${{A}_{1}}{{B}_{1}}{{C}_{1}}$

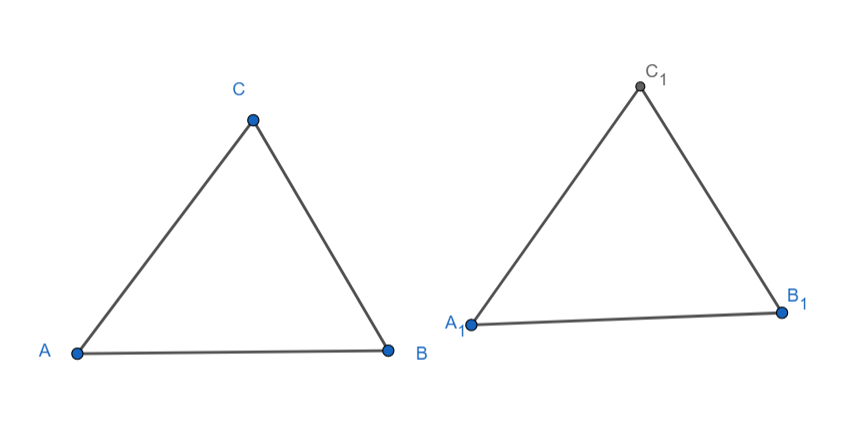
Let $\angle B=\angle {{B}_{1}}=90{}^\circ ,\angle C=\angle {{C}_{1}}=110{}^\circ ,BC={{B}_{1}}{{C}_{1}}=5.2cm$
Hence in triangles $ABC$ and ${{A}_{1}}{{B}_{1}}{{C}_{1}}$, we have
$\begin{align}
  & BC={{B}_{1}}{{C}_{1}} \\
 & \angle B=\angle {{B}_{1}} \\
 & \angle C=\angle {{C}_{1}} \\
\end{align}$
Hence by ASA congruence criterion, we have $\Delta ABC\cong \Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}$
Hence if the triangle exists, it will be unique.
But, we have $\angle B+\angle C=90{}^\circ +110{}^\circ =200{}^\circ > 180{}^\circ $
Hence it is not possible to construct a triangle with given parameters
Consider two triangles XYZ and ${{X}_{1}}{{Y}_{1}}{{Z}_{1}}$

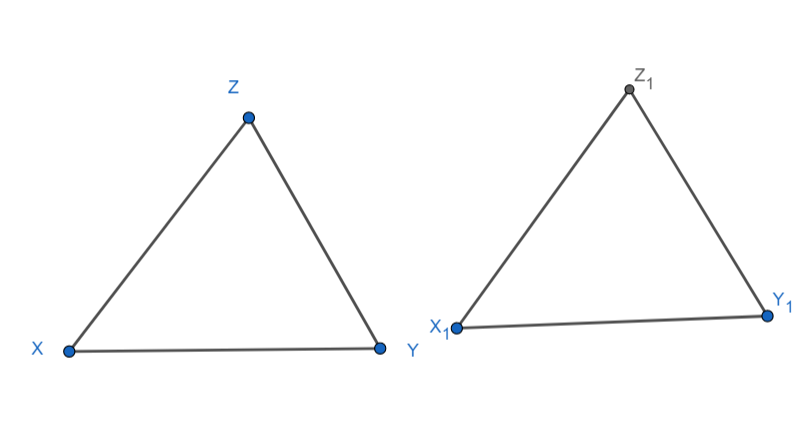
Let $XY={{X}_{1}}{{Y}_{1}}=5cm,\angle X=\angle {{X}_{1}}=45{}^\circ ,\angle Y=\angle {{Y}_{1}}=60{}^\circ $
Hence, in triangles XYZ and ${{X}_{1}}{{Y}_{1}}{{Z}_{1}}$, we have
$\begin{align}
  & \angle X=\angle {{X}_{1}} \\
 & XY={{X}_{1}}{{Y}_{1}} \\
 & \angle Y=\angle Y \\
\end{align}$
Hence by ASA congruence criterion $\Delta XYZ\cong \Delta {{X}_{1}}{{Y}_{1}}{{Z}_{1}}$
Hence if the triangle exists, it will be unique.
Also, we have $\angle X+\angle Y=60{}^\circ +45{}^\circ =105{}^\circ <180{}^\circ $
Hence it is possible to construct a triangle with given conditions.
Consider two isosceles triangles with side lengths as 6.2cm, 6.2cm, 6.2cm and 6.2cm,6.2cm, 4cm.
 Clearly, both the triangles satisfy option [d]. But since the third side length is not equal in both the triangles, the triangles are not congruent. Also, it is possible to construct triangles with these side lengths since the sum of any two sides is greater than the third side.
Hence option [c] is the only correct option.

Note: The most common mistake made by students in these types of questions is that they forget to verify various properties of a triangle like angle sum property, the sum of two sides is greater than the third side etc. and hence end up with incorrect results. One can also verify the above results by trying to construct these triangles with known construction methods and infer results from there.