Question

In what ratio must a grocer mix two varieties of tea worth Rs 60 per kg and Rs 65 per kg so that by selling the mixture at Rs 68.20 a kg he may gain 10%?
A. \[3:2\]
B. \[3:4\]
C. \[3:5\]
D. \[4:5\]

Answer 1

Hint: Here Percentage gain means to express the profit or the gain in the form of percentages. And remind that the price paid by the retailer for the goods that he is going to sell is called the cost price and the price at which he is selling that goods to the consumers is called the selling price.

Complete step-by-step answer:
Given Selling price (SP) of 1 kg of the mixture = Rs 68.20
Percentage of profit or gain = 10%
We know that cost price \[CP = \dfrac{{SP \times 100}}{{100 + Gain\% }}\]
\[
  CP = \dfrac{{68.20 \times 100}}{{100 + 10}} \\
    \\
  CP = \dfrac{{6820}}{{110}} \\
    \\
  \therefore CP = Rs{\text{ }}62 \\
\]
Given cost of 1 kg tea of first kind = Rs 60
Cost of 1 kg tea of second kind = Rs 65
So, the mean price \[ = \dfrac{{60 + 65}}{2} = 62.50 \cong R{\text{s 62}}\]
By the rule of allegation, we have

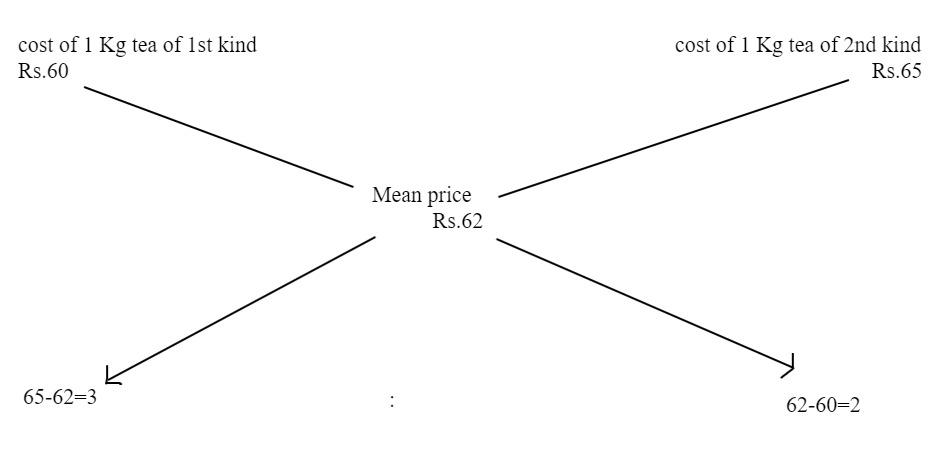
Therefore, the required ratio is \[3:2\]
Thus, the correct option is A. \[3:2\].

Note: In this problem we have used the rule of allegation. The rule of allegation states that “when different quantities of different ingredients are mixed together to produce a mixture of a mean value, the ratio of their quantities is inversely proportional to the differences in their cast from the mean value”.