
In what ratio is the line joining $\text{A}\left( 8,9 \right)$ and $\text{B}\left( -7,4 \right)$ is divided by
(a). The point $\left( 2,7 \right)$
(b). The x-axis
(c). The y-axis
Answer
608.1k+ views
Hint: suppose, the ratio in all cases lying on the line joining given as \[k:1\]. Use sectional formula given for calculating a point which divides the line segment joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$in the ratio \[m:n\]; point given as \[\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] any point on x-axis has y-coordinates as 0 and vice-versa is also true. Use this logic to solve the problem.
Complete step-by-step answer:
We know the point which divides the line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in ratio of \[m:n\], is given by sectional formula as:-
\[\text{R}\ =\ \left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] …………………………………………(i)
Now, coming to the question, we need to find the ratio by which line joining $\text{A}\left( 8,9 \right)$ and $\text{B}\left( -7,4 \right)$ would be divided by the given points in the axis.
(a). The point $\left( 2,7 \right)$
Let us suppose $\left( 2,7 \right)$ divides the line joining $\left( 8,9 \right)$and $\left( -7,4 \right)$ in ratio of \[k:1\].
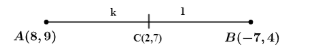
Now, we can get coordinates of c with the help of equation (i), where
\[m=k\], \[n=1\] and \[\left( {{x}_{1}},{{y}_{1}} \right)\ =\ \left( 8,9 \right)\], \[\left( {{x}_{2}},{{y}_{2}} \right)\ =\ \left( -7,4 \right)\]
So, we get coordinated of c as
\[c\ =\ \left( \dfrac{-7k+8}{k+1},\dfrac{4k+9}{k+1} \right)\]
Now, it is given that coordinates of point c is $\left( 2,7 \right)$, So, we get,
\[\dfrac{-7k+8}{k+1}\ =\ 2\] and \[\dfrac{4k+9}{k+1}\ =\ 7\]
\[-7k+8\ =\ 2k+2\] and \[4k+9\ =\ 7k+7\]
\[9k\ =\ 6\] and \[3k\ =\ 2\]
\[k\ =\ \dfrac{6}{9}\ =\ \dfrac{2}{3}\] and \[k\ =\ \dfrac{2}{3}\]
Hence, ratio \[k:1\]is given as \[2:3\].
So, point $\left( 2,7 \right)$ will divide the line joining the given points in ratio of \[2:3\].
(b). The x- axis
Let us suppose that any coordinate on the x-axis will divide the line joining the given points in ratio \[k:1\].
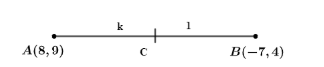
Let us suppose the point on the x-axis is represented by ‘c’.
So, coordinates of c can be given with the help of equation (i) as
\[c\ =\ \left( \dfrac{-7k+8}{k+1},\dfrac{4k+9}{k+1} \right)\]
As, the point c is lying on the x-axis, so y-coordinate of this point should be 0 because y-coordinate of any point at x-axis is 0.
So, put the y-coordinate of point c to 0, to get the value of k.
So, we get
\[\dfrac{4k+9}{k+1}\ =\ 0\]
Or \[4k+9\ =\ 0\]
\[k\ =\ -\dfrac{9}{4}\]
Hence, line joining by the point given points will be divided by x-axis in ratio of \[9:4\] externally as the value of k is negative.
(c). The y-axis
So, we can use the previous coordinate of ‘c’. and put the x-coordinate of point c to 0, as x-coordinate on y-axis will be 0.
Hence, we get
\[\dfrac{-7k+8}{k+1}\ =\ 0\]
\[-7k+8\ =\ 0\]
\[7k\ =\ 8\]
\[k\ =\ \dfrac{8}{7}\]
So, the y-axis will divide the line joining the given points in ratio of \[8:7\].
Note: please take care with the positions of $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and m and n in the sectional formula. One may go wrong if he/she applies this formula as \[\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] using the concept that x-coordinate of any point on y-axis is 0 and y-coordinate of any point on x-axis is 0 are the key points with the second and third party of the question.
Negative value of k suggests that the point dividing it in \[k:1\] will not lie in between the line segments, it will divide the line externally, not internally.
Complete step-by-step answer:
We know the point which divides the line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in ratio of \[m:n\], is given by sectional formula as:-
\[\text{R}\ =\ \left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] …………………………………………(i)
Now, coming to the question, we need to find the ratio by which line joining $\text{A}\left( 8,9 \right)$ and $\text{B}\left( -7,4 \right)$ would be divided by the given points in the axis.
(a). The point $\left( 2,7 \right)$
Let us suppose $\left( 2,7 \right)$ divides the line joining $\left( 8,9 \right)$and $\left( -7,4 \right)$ in ratio of \[k:1\].
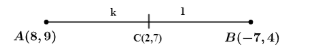
Now, we can get coordinates of c with the help of equation (i), where
\[m=k\], \[n=1\] and \[\left( {{x}_{1}},{{y}_{1}} \right)\ =\ \left( 8,9 \right)\], \[\left( {{x}_{2}},{{y}_{2}} \right)\ =\ \left( -7,4 \right)\]
So, we get coordinated of c as
\[c\ =\ \left( \dfrac{-7k+8}{k+1},\dfrac{4k+9}{k+1} \right)\]
Now, it is given that coordinates of point c is $\left( 2,7 \right)$, So, we get,
\[\dfrac{-7k+8}{k+1}\ =\ 2\] and \[\dfrac{4k+9}{k+1}\ =\ 7\]
\[-7k+8\ =\ 2k+2\] and \[4k+9\ =\ 7k+7\]
\[9k\ =\ 6\] and \[3k\ =\ 2\]
\[k\ =\ \dfrac{6}{9}\ =\ \dfrac{2}{3}\] and \[k\ =\ \dfrac{2}{3}\]
Hence, ratio \[k:1\]is given as \[2:3\].
So, point $\left( 2,7 \right)$ will divide the line joining the given points in ratio of \[2:3\].
(b). The x- axis
Let us suppose that any coordinate on the x-axis will divide the line joining the given points in ratio \[k:1\].

Let us suppose the point on the x-axis is represented by ‘c’.
So, coordinates of c can be given with the help of equation (i) as
\[c\ =\ \left( \dfrac{-7k+8}{k+1},\dfrac{4k+9}{k+1} \right)\]
As, the point c is lying on the x-axis, so y-coordinate of this point should be 0 because y-coordinate of any point at x-axis is 0.
So, put the y-coordinate of point c to 0, to get the value of k.
So, we get
\[\dfrac{4k+9}{k+1}\ =\ 0\]
Or \[4k+9\ =\ 0\]
\[k\ =\ -\dfrac{9}{4}\]
Hence, line joining by the point given points will be divided by x-axis in ratio of \[9:4\] externally as the value of k is negative.
(c). The y-axis
So, we can use the previous coordinate of ‘c’. and put the x-coordinate of point c to 0, as x-coordinate on y-axis will be 0.
Hence, we get
\[\dfrac{-7k+8}{k+1}\ =\ 0\]
\[-7k+8\ =\ 0\]
\[7k\ =\ 8\]
\[k\ =\ \dfrac{8}{7}\]
So, the y-axis will divide the line joining the given points in ratio of \[8:7\].
Note: please take care with the positions of $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and m and n in the sectional formula. One may go wrong if he/she applies this formula as \[\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\] using the concept that x-coordinate of any point on y-axis is 0 and y-coordinate of any point on x-axis is 0 are the key points with the second and third party of the question.
Negative value of k suggests that the point dividing it in \[k:1\] will not lie in between the line segments, it will divide the line externally, not internally.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




