
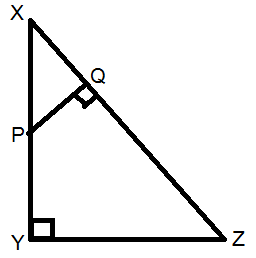
In $\vartriangle XYZ$, P is any point on XY and $PQ \bot XZ$. If XP = 4 cm, XY = 16 cm and XZ = 24 cm, find XQ.

Answer
595.2k+ views
Hint:
Two figures having the same shape but not necessarily same size, are called similar figures.
Here in the question, the unknown XQ and XP are the parts of $\vartriangle XQP$and similarly XY and YZ are the parts of another triangle $\vartriangle XYZ$. Try to prove these triangles similar. Because:
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
This criterion is referred to as AAA (Angle-Angle-Angle) criterion of similarity of two triangles.
The similarity of two triangles should be expressed symbolically, using correct correspondence of their vertices.
Complete step by step solution:
Step 1: Draw the given figure
Step 2: given that
XP = 4 cm, XY = 16 cm and XZ = 24 cm,
$PQ \bot XZ$
$ \Rightarrow \angle PQX = 90^\circ $ …… (1)
$XY \bot YZ$
$ \Rightarrow \angle XYZ = 90^\circ $ …… (2)
Step 3: prove the similarity of triangles $\vartriangle XQP{\text{ and }}\vartriangle XYZ$
In $\vartriangle XQP{\text{ and }}\vartriangle XYZ$,
$\angle PQX = \angle XYZ = 90^\circ $ (from (1) and (2)
$\angle PXQ = \angle ZXY$ (common)
Hence, $\vartriangle XQP{\text{ }} \sim {\text{ }}\vartriangle XYZ$ by AAA similarity criterion of two triangles
Corresponding ratios of similar triangles are equal:
$ \Rightarrow \dfrac{{XQ}}{{XY}} = \dfrac{{QP}}{{YZ}} = \dfrac{{XP}}{{XZ}}$
Step 6: Substituting the given values XP = 4 cm, XY = 16 cm and XZ = 24 cm,
$
\Rightarrow \dfrac{{XQ}}{{XY}} = \dfrac{{XP}}{{XZ}} \\
\Rightarrow \dfrac{{XQ}}{{16}} = \dfrac{4}{{24}} \\
\Rightarrow XQ = \dfrac{4}{{24}} \times 16 \\
$
$
\Rightarrow XQ = \dfrac{8}{3} \\
\Rightarrow XQ = 2.67cm \\
$
Therefore, the length of XQ is 2.67cm.
Note:
Always remember questions including ratios of sides of two triangles, the triangles must be similar. Use AAA or AA criterion of similarity of two triangles.
If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal.
Therefore, AAA similarity criterion can also be stated as follows:
If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. This criterion is referred to as AA (Angle-Angle) criterion of similarity of two triangles.
Students get confused between similar figures and congruent figures. Let’s understand the difference by an example:
All the circles are similar to other circles, but only those circles having the same radius are congruent.
Two figures having the same shape but not necessarily same size, are called similar figures.
Here in the question, the unknown XQ and XP are the parts of $\vartriangle XQP$and similarly XY and YZ are the parts of another triangle $\vartriangle XYZ$. Try to prove these triangles similar. Because:
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
This criterion is referred to as AAA (Angle-Angle-Angle) criterion of similarity of two triangles.
The similarity of two triangles should be expressed symbolically, using correct correspondence of their vertices.
Complete step by step solution:
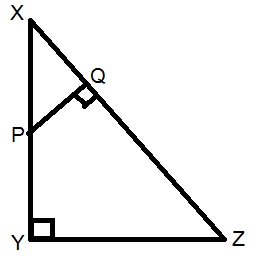
Step 1: Draw the given figure

Step 2: given that
XP = 4 cm, XY = 16 cm and XZ = 24 cm,
$PQ \bot XZ$
$ \Rightarrow \angle PQX = 90^\circ $ …… (1)
$XY \bot YZ$
$ \Rightarrow \angle XYZ = 90^\circ $ …… (2)
Step 3: prove the similarity of triangles $\vartriangle XQP{\text{ and }}\vartriangle XYZ$
In $\vartriangle XQP{\text{ and }}\vartriangle XYZ$,
$\angle PQX = \angle XYZ = 90^\circ $ (from (1) and (2)
$\angle PXQ = \angle ZXY$ (common)
Hence, $\vartriangle XQP{\text{ }} \sim {\text{ }}\vartriangle XYZ$ by AAA similarity criterion of two triangles
Corresponding ratios of similar triangles are equal:
$ \Rightarrow \dfrac{{XQ}}{{XY}} = \dfrac{{QP}}{{YZ}} = \dfrac{{XP}}{{XZ}}$
Step 6: Substituting the given values XP = 4 cm, XY = 16 cm and XZ = 24 cm,
$
\Rightarrow \dfrac{{XQ}}{{XY}} = \dfrac{{XP}}{{XZ}} \\
\Rightarrow \dfrac{{XQ}}{{16}} = \dfrac{4}{{24}} \\
\Rightarrow XQ = \dfrac{4}{{24}} \times 16 \\
$
$
\Rightarrow XQ = \dfrac{8}{3} \\
\Rightarrow XQ = 2.67cm \\
$
Therefore, the length of XQ is 2.67cm.
Note:
Always remember questions including ratios of sides of two triangles, the triangles must be similar. Use AAA or AA criterion of similarity of two triangles.
If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal.
Therefore, AAA similarity criterion can also be stated as follows:
If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar. This criterion is referred to as AA (Angle-Angle) criterion of similarity of two triangles.
Students get confused between similar figures and congruent figures. Let’s understand the difference by an example:
All the circles are similar to other circles, but only those circles having the same radius are congruent.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




