Question

In $\vartriangle PQR$, $E$ and $F$ are points on the sides $PQ$ and $PR$ respectively. Verify $EF||QR,PQ = 1.28cm,PR = 2.56cm,PE = 0.18cm,PF = 0.36cm$

Answer 1

Hint: In such type of question the concept of basic proportionality is taken into consideration which states that if we draw a line from one side of a triangle to the other side of the triangle and it intersects at two different points then it divided the side in same ratios, using this theorem if we need to show that the side is parallel then in such case we will show that they have same ratio when two points are taken.

Complete step-by-step answer:
Let us consider a triangle, $E$ and $F$ be the point on the sides of the triangle as shown in the below figure

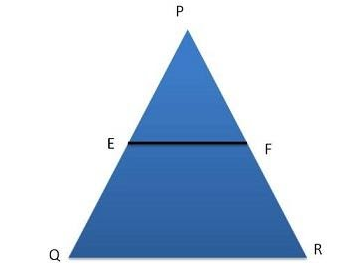
Now, as discussed we need to show that the ratio is same as shown below
$\Rightarrow$$\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}}$
And we need to have the length of the above
Let us first consider the side $PQ$
$\Rightarrow$$PQ = PE + ER$
It is given that $PQ = 1.28cm$ and $PE = 0.18cm$
Substituting the values we get
$\Rightarrow$$EQ = 1.28 - 0.18 = 1.10cm$
Now, we can determine the ration for the side $PQ$
$\Rightarrow$$\dfrac{{PE}}{{EQ}} = \dfrac{{0.18}}{{0.10}} = 0.16$
Now, let us consider the other side of the triangle $PR$
$PR = PF + FR$
Substituting the value, we get
$\Rightarrow$$FR = PR - PF = 2.56 - 0.36 = 2.20cm$
Now, we need to determine the ratio of the side $PR$
$\Rightarrow$$\dfrac{{PF}}{{FR}} = \dfrac{{0.36}}{{2.20}} = 0.16$
Hence, they both have the same ratio
$\Rightarrow$$\dfrac{{PE}}{{EQ}} = \dfrac{{PF}}{{FR}} = 0.16$
Hence, by the proportionality theorem we can say that $EF||QR$.

Note: If the side of a triangle is divide in two parts as in the above question we represent the side of a triangle by the sum of two lines as shown in the diagram $PQ = PE + ER$ and we have have information of length of $PQ$ and $PF$ then in such case we can determine the length of the side for which we don’t have any information.