Question

In \[\vartriangle PQR\] , \[\angle P = 70^\circ \] and \[\angle R = 30^\circ \] . Which side of this triangle is longest? Give Reason.

Answer 1

Hint:In the above given question, we are given a triangle, which is \[\vartriangle PQR\] . In the given triangle \[\vartriangle PQR\] we have \[\angle P = 70^\circ \] and \[\angle R = 30^\circ \] . We have to determine which side of this triangle is the longest. In order to approach the solution, we have to recall the property of a triangle that the side opposite to a greater angle is larger. Also, using the angle sum property of a triangle, we can find the third angle of the given triangle \[\vartriangle PQR\].

Complete step by step answer:
Given that, a \[\vartriangle PQR\] in which \[\angle P = 70^\circ \] and \[\angle R = 30^\circ \]. We have to determine the longest side of the triangle \[\vartriangle PQR\]. Now since two angles of the triangle \[\vartriangle PQR\] are given, hence we can find the third angle of \[\vartriangle PQR\] using the angle sum property of a triangle.

From the angle sum property of \[\vartriangle PQR\] , we have
\[ \Rightarrow \angle P + \angle Q + \angle R = 180^\circ \]
That gives us,
\[ \Rightarrow 70^\circ + \angle Q + 30^\circ = 180^\circ \]
\[ \Rightarrow \angle Q = 180^\circ - 100^\circ \]
Hence,
\[ \Rightarrow \angle Q = 80^\circ \]
So the three angles of the triangle \[\vartriangle PQR\] are \[\angle P = 70^\circ \] , \[\angle Q = 80^\circ \] , and \[\angle R = 30^\circ \]. Hence, the figure of the triangle \[\vartriangle PQR\] can be drawn as the triangle shown below.

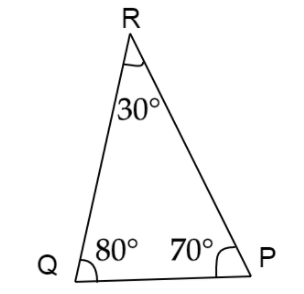
Now, since we know the values of all the three angles of the triangle \[\vartriangle PQR\] , hence by using the property of a triangle that the side opposite to the greater angles is larger, we can determine the longest side of the triangle \[\vartriangle PQR\].

In the triangle \[\vartriangle PQR\] , the largest angle is \[\angle Q\] which has the highest measure of \[80^\circ \]. Therefore, the side opposite to \[\angle Q\] must be the longest side in the triangle \[\vartriangle PQR\]. Since, the side opposite to the angle \[\angle Q\] in the triangle \[\vartriangle PQR\] is \[PR\].

Hence \[PR\] is the longest side of \[\vartriangle PQR\].

Note:In the above given problem, the given triangle \[\vartriangle PQR\] has three different i.e. unequal angles as \[\angle P = 70^\circ \] , \[\angle Q = 80^\circ \] , and \[\angle R = 30^\circ \] . That implies the triangle \[\vartriangle PQR\] has three unequal sides \[PQ\] , \[QR\] and \[PR\] . Therefore, the given triangle \[\vartriangle PQR\] is a scalene triangle.