Question

In \[\vartriangle {\text{LTR~}}\vartriangle {\text{HYD}}\]\[\vartriangle {\text{HYD}}\] is such that \[{\text{HY}} = 7.2{\text{cm}}\],\[{\text{YD}} = 6{\text{cm}}\],\[\angle {\text{Y}} = 40\]
\[\dfrac{{{\text{LR}}}}{{{\text{HD}}}} = \dfrac{5}{6}\] . Construct\[\vartriangle {\text{LTR}}\].

Answer 1

Hint: We know that a triangle is a three-sided polygon. It has three sides, three vertices and three angles. Also a triangle can be constructed if:
(i) all three sides are given
(ii) two sides and included angle are given
(iii) two angles and the included side is given
(iv) the measure of the hypotenuse and a side is given in the right triangle.
So by using the above information we can construct a triangle

Complete step by step answer:
Given
\[
  \vartriangle {\text{LTR~}}\vartriangle {\text{HYD}}..................................\left( i \right) \\
  \vartriangle {\text{HYD}} \\
  {\text{HY}} = 7.2{\text{cm}},{\text{YD}} = 6{\text{cm,}}\angle {\text{Y}} = 40,\dfrac{{{\text{LR}}}}{{{\text{HD}}}} = \dfrac{5}{6}...........................\left( {ii} \right) \\
 \]
Now using the above information we should construct the \[\vartriangle {\text{LTR}}\].
Now to construct \[\vartriangle {\text{LTR}}\] we need to know the following:
\[{\text{LT,}}{\text{TR,}}\angle {\text{T}}\]
Now we it’s also given \[\dfrac{{{\text{LR}}}}{{{\text{HD}}}} = \dfrac{5}{6}\] such that the sides of the triangle \[\vartriangle {\text{LTR}}\]would be $\dfrac{5}{6}$ times the \[\vartriangle {\text{HYD}}\]
So first let’s find ${\text{LT}}$ :
Since \[\dfrac{{{\text{LR}}}}{{{\text{HD}}}} = \dfrac{5}{6}\] and \[\vartriangle {\text{LTR~}}\vartriangle {\text{HYD}}\]
We can write:
\[
  {\text{LT = }}\dfrac{5}{6} \times 7.2 \\
  {\text{LT = }}\dfrac{{36}}{6} \\
  {\text{LT = }}6{\text{cm}}..............................\left( {iii} \right) \\
 \]

Now let’s find${\text{TR}}$ :
Since \[\dfrac{{{\text{LR}}}}{{{\text{HD}}}} = \dfrac{5}{6}\] and \[\vartriangle {\text{LTR~}}\vartriangle {\text{HYD}}\]
We can write:
\[
  {\text{TR = }}\dfrac{5}{6} \times 6 \\
  {\text{TR = }}\dfrac{{30}}{6} \\
  {\text{TR = 5cm}}..............................\left( {iv} \right) \\
 \]
Now let’s find \[\angle {\text{T}}\]:
Since \[\vartriangle {\text{LTR~}}\vartriangle {\text{HYD}}\]
We can write:
\[\angle {\text{T}} = \angle Y = 40.....................\left( v \right)\]
Now since we have found \[{\text{LT,}}{\text{TR,}}\angle {\text{T}}\] let’s construct\[\vartriangle {\text{LTR}}\].
Steps of construction:
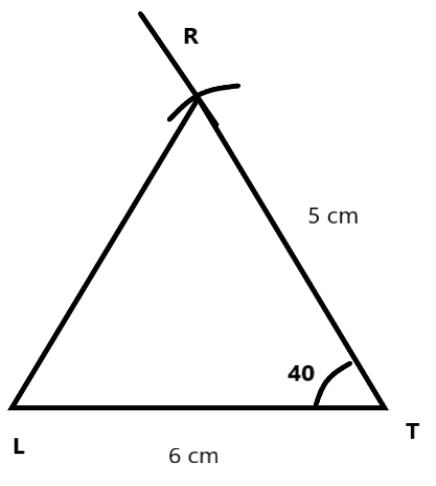
Step 1: Draw base \[{\text{LT}} = 6cm\] with a scale.
Step 2: Draw a line at an angle of ${40^ \circ }$ from point ${\text{T}}$.
Step 3: Place the compass on point ${\text{T}}$ and draw an arc of length of \[5cm\] .
Step 4: Mark the intersection point of the line and arc in steps 2 and 3 as point ${\text{R}}$ and draw lines joining ${\text{R - L}}\,{\text{and}}{\text{R - T}}$.
So on constructing \[\vartriangle {\text{LTR}}\] we get:

Note: On dealing with problems of construction one should be careful with the properties of similar triangles as well as that of congruency. Also while constructing a triangle one should take care while taking the measurements since there are chances for discrepancies.