Question

In $ \vartriangle ABC $ , the bisector of $ \angle A $ intersects BC in D, if $ AB = 18 $ cm, $ AC = 15 $ cm and $ BC = 22 $ cm, find BD.

Answer 1

Hint: In order to determine the value of BD , use the angle bisector theorem as $ \dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}} $ . DC can be rewritten as BC-BD, put into the equation. Now put the value of AB,AC, and BC into the equation. Cross-multiply the equation and combine all the like terms to get the value of BD.

Complete step by step solution:
We are given a triangle $ \Delta ABC $ having sides $ AB = 18 $ cm, $ AC = 15 $ cm and $ BC = 22 $ cm and an angle bisector of $ \angle A $ which meet the opposite side BC at point D.

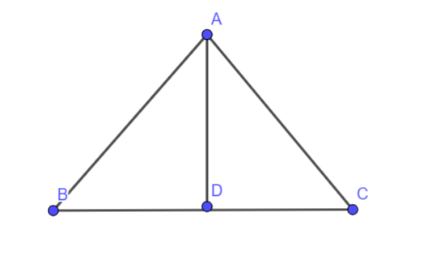
We have to find the value of BD.
Since, AD is the angle bisector of $ \angle A $ , so by angle bisector theorem which states that an angle bisector of any triangle divides the opposite side into two pieces of segments which are proportional to the other two sides of the given triangle.
In our case, the segments of BC are BD and DC and the other two sides of the triangle $ \Delta ABC $ are AB and AC.
So, by angle bisector theorem we can write
 $ \dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{DC}} $
 $ DC $ can be written as $ DC = BC - BD $ , we get
 $ \dfrac{{AB}}{{AC}} = \dfrac{{BD}}{{BC - BD}} $
Putting the value of AB,AC, and BC, our equation becomes
 $
  \dfrac{{18}}{{15}} = \dfrac{{BD}}{{22 - BD}} \\
  \dfrac{6}{5} = \dfrac{{BD}}{{22 - BD}} \;
  $
Cross-multiplying the terms,
\[6\left( {22 - BD} \right) = 5 \times BD\]
Using the distributive law of multiplication in the left-hand side to multiply the terms as $ A\left( {B + C} \right) = AB + AC $ , we get our equation as
\[132 - 6BD = 5BD\]
Transposing terms having BD from LHS to RHS and combining them
\[
  132 = 5BD + 6BD \\
  132 = 11BD \;
 \]
Dividing both sides of the equation with the coefficient of BD i.e. with the number $ 11 $
\[
  \dfrac{{132}}{{11}} = \dfrac{{11BD}}{{11}} \\
  BD = 12\,cm \;
 \]
Therefore, the value of BD is equal to $ 12cm $ .
So, the correct answer is “$ 12cm $”.

Note: 1. Remember to place the correct length unit for the value of BD. In our question, length is given in $ cm $ .
2. Make sure you write the angle-bisector theorem properly.
3. Angle bisector of any angle is a line which splits the given angle into two equal angles.
4. Value for DC can be obtained by calculating $ BC - BD $ .
5. To cross check your result , you can check $ BC = BD + DC $ by putting the values.