Question

In \[\vartriangle ABC\], AB$ = $5 cm, BC$ = $6 cm, AC$ = $4 cm. Identify the type of triangle.
A.Right angled triangle
B.Isosceles triangle
C.Equilateral triangle
D.Scalene triangle

Answer 1

Hint: Here, we are required to identify the type of the given triangle. We would use the properties of different types of triangles to answer this question. We would check that the given sides of the triangle satisfy the properties of which triangle, hence, that would be the required answer.

Complete step-by-step answer:
In a triangle, the sum of any two sides is always greater than the third side. Hence, first of all, we would show whether AB, BC and AC form a triangle or not.

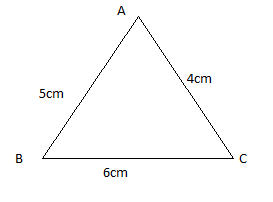
1.AB$ + $BC$ = $$\left( {5 + 6} \right) = 11$cm$ > $4 cm (AC)
2.BC$ + $AC$ = $$\left( {6 + 4} \right) = 10$cm$ > $5 cm (AB)
3.AB$ + $AC$ = $$\left( {5 + 4} \right) = 9$cm$ > $6 cm (BC)
Clearly, the sum of any two sides is always greater than the third side.
Hence, these lengths form a triangle.
Now, since all the sides are of different length,
Hence, this is a scalene triangle.
For right angled triangle:
The sum of squares of two sides should be equal to the square of the largest side.
Here, largest side is BC$ = $6 cm
Hence,
LHS: ${\left( {AB} \right)^2} + {\left( {AC} \right)^2}$
$ = {\left( 5 \right)^2} + {\left( 4 \right)^2}$
$ = 25 + 16 = 41$
RHS: ${\left( {BC} \right)^2}$
$ = {\left( 6 \right)^2} = 36$
Clearly, LHS$ \ne $RHS
Hence, this is not a right angled triangle.
Hence, Option A is rejected.
Now, since, all the three sides are different
Hence, the given triangle can’t be an equilateral triangle as in an equilateral triangle; all the three sides are of the same length.
Similarly, it can’t be an isosceles triangle because in an isosceles triangle, two sides are equal and only one side is different.
Therefore, option D is the correct option.
The given \[\vartriangle ABC\] is a scalene triangle.

Note: To answer this question, it is really important to check whether the given sides form a triangle or not. This is because if in the options we had ‘none of these’ then, it could arise a chance of the sides not forming a triangle. Hence, we should know how to check for a triangle. Then, applying the properties of different triangles correctly would help us know the type of the given triangle.