Question

In two right triangles one side and an acute angle of one are equal to the corresponding side and angle of the other. Prove that the triangles are congruent.

Answer 1

Hint: The Angle-Angle-Side criteria (AAS) specifies that if any two angles and a opposite of any one of the angle is given then triangles can be equated or can form congruence when two angles and side is common value in both the triangles like given in the diagram below:

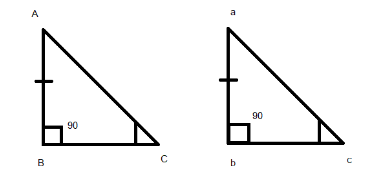
where \[\angle C=\angle c\] and AB is equal to ab.

Complete step-by-step answer:
To prove congruency one must form equal angles or/and side with another triangle. In case when two angles and a side are the same then we can say that the triangles are in AAS congruency or Angle-Angle-Side congruence. There is a difference between AAS (Angle-Angle-Side) and ASA (Angle- Side- Angle) with ASA, the side which is equal in both tends to have the two angles which are similar in both the triangles like shown below:

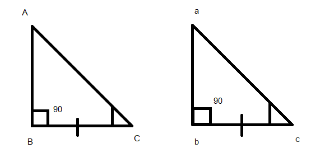
Here the sides and the angles are in same section or part whereas in AAS as shown below:

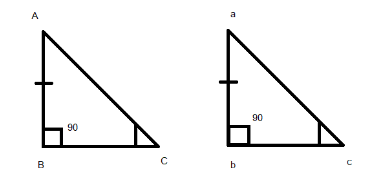
The sides are corresponding to the angles given in the above diagram. Hence by AAS criteria we can say that the angle \[\angle ABC=\angle abc\] , \[\angle ACB=\angle acb\] and sides AB is equal to ab. Therefore, yes both the triangles are congruent on the basis of AAS (Angle-Angle-Side).

Note: Students may think both ASA and AAS are same but in hindsight both are different as the side’s position is different in both of them and the most appropriate congruency in this case is that of AAS.