Question

In $\triangle\mathrm{ABC}\;,\;\mathrm{AC}=4\mathrm x,\;\mathrm{BC}=6\mathrm x-6,\;\mathrm{AB}=5\mathrm x-8\;\mathrm{and}\;\angle\mathrm A=\angle\mathrm B.\;$ Find the perimeter of $\triangle\mathrm{ABC}$.

Answer 1

Hint: The perimeter of a triangle is equal to the sum of its sides. Also, the knowledge of an isosceles triangle is required to solve this problem. The given triangle is an isosceles triangle as two of its angles are equal. In an isosceles triangle, the sides opposite to equal angles are also equal.

Complete step by step answer:
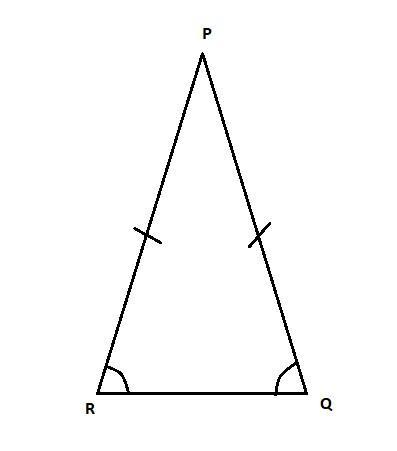
This is an example of isosceles triangle with $\angle\mathrm Q=\angle\mathrm R$ and PR=PQ
We have been given the sides of a triangle ABC which is isosceles. The figure for the triangle is given below-

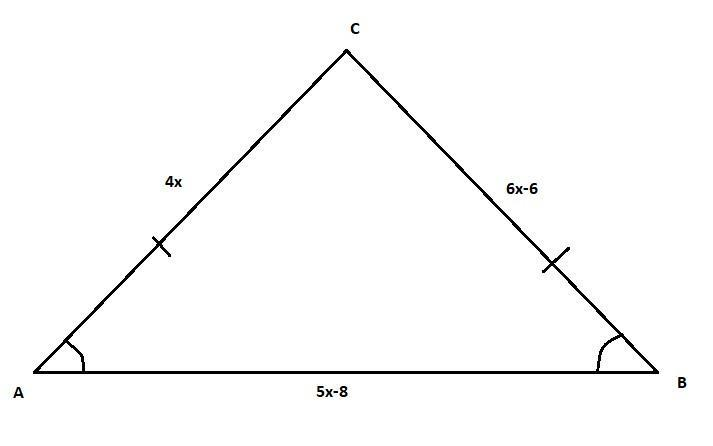
Using the properties of the isosceles triangle, since$\angle\mathrm A=\angle\mathrm B$, the opposite sides AC and BC will be equal. Hence, we can equate the length of the two sides and find the value of x.
AC = BC
4x = 6x - 6
2x = 6
x = 3 units …(1)
With the value of x, the sides of the triangle can be calculated using equation (1) -
AB = 5x - 8 = 15 - 8 = 7 units ….(2)
BC = 6x - 6 = 18 - 6 = 12 units ……(3)
AC = 4x = 12 units …….(4)
The perimeter of a triangle is defined as the sum of its sides. So the perimeter P wil be-
P = AB + BC + AC
Substituting the values using equations (2), (3) and (4)-
P = 7 + 12 + 12
P = 31 units

This is the required answer.

Note: Students often do not write the units if they are not mentioned. So, the units should be written even if they are not mentioned in the question. In geometry questions of such type, a diagram should be drawn with proper labellings to explain the answer.