Question

In triangle \[ABC,\angle A = \dfrac{\pi }{3}\] and it’s encircle is of units radius. If the radius of the circle touching the sides \[AB,AC\] internally and encircle externally is x, then the value of x is
(A) \[\dfrac{1}{2}\]
(B) \[\dfrac{1}{4}\]
(C) \[\dfrac{1}{3}\]
(D) None of these

Answer 1

Hint: First, we have to draw a circle with the given conditions. Then we compare the sides and angles for some similarity using trigonometric values and solve for \[x\]and \[y\]. An acute angle is extensively used in this solution.

Complete answer:
First, we draw a circle with a unit radius.

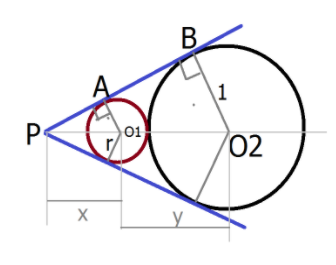
Secondly, we mark the radius as 1 with center \[o2\]
Forming a triangle ABC we see that the circle with unit radius touches the circle at abs and AC
Again we draw an encircle with radius x with center \[o1\]
Hence we get the above diagram
From the above diagram we get right-angled triangles \[APO1\] AND \[ABO2\]
Hence we can write it as
\[(x + y)\sin (30) = 1\]
We write \[\sin (30)\]because the angle formed is \[\sin (30)\]
Hence we know that \[\sin 30 = \dfrac{1}{2}\]
Substituting the values we get,
\[(x + y)\sin 30 = 1\]
\[(x + y)\dfrac{1}{2} = 1 \]
 \[x + y = 2 \]
Again we know that
\[x\sin 30 = r\]
Because the angle formed by the encircling has a radius \[r\]
Therefore we have:
\[x = 2r\]
Again for \[y = 1 + r\]
Solving this we get
\[x + y = 2 \]
\[2r + 1 + r = 2 \]
\[3r + 1 = 2 \]
\[3r = 2 - 1 \]
\[3r = 1 \]
\[r = \dfrac{1}{3} \]

Hence the correct option is (C) i.e. \[\dfrac{1}{3}\]

Additional information:
Triangles and their properties are an essential part of solving questions as such. The trigonometric application adds to the sum to give the final answer.

Note:
Geometry and construction of triangles should be clear along with a clear understanding of their properties and formulas. Trigonometric formula i.e. \[\sin (30)\]is an essential part to proceed as it forms an angle with the triangle. The knowledge of adjacent sides along with values of trigonometric is essential.