Question

In triangle ABC, XY||AC and divides the triangle into two parts of equal areas. Find the ratio of AX and AB.

Answer 1

Hint: In this question, properties of similar triangles will be used. The properties state that-
The corresponding sides of similar triangles are in proportion. …(1)
The areas of similar triangles are in proportion to the square of their corresponding sides. …(2)

Complete step-by-step answer:
The figure of the triangle is as follows-

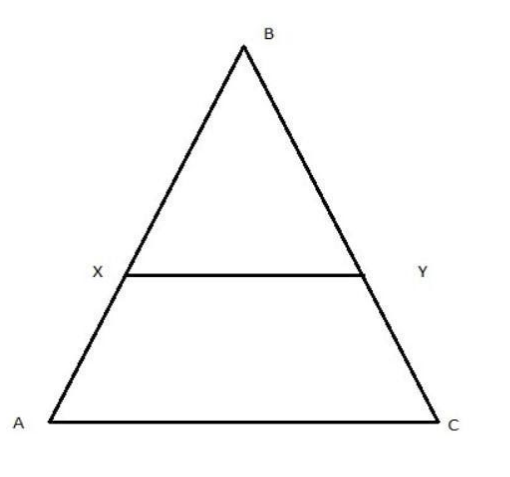
XY||AC and ar(AXYC)=ar(BXY)
So, ar(∆ACB) = 2ar(∆XYB)...(3)

In ∆ABC and ∆XBY,
$\angle\mathrm B\;\mathrm{is}\;\mathrm{common}\\\mathrm{XY}\vert\vert\mathrm{AC},\;\mathrm{so}\;\angle\mathrm{BXY}\;\mathrm{and}\;\angle\mathrm{BAC}\;\mathrm{are}\;\mathrm{corresponding}\;\mathrm{angles}\\\angle\mathrm{BXY}=\angle\mathrm{BAC}$

By AA similarity,
∆ABC~∆XBY
Hence, by corresponding parts of similar triangles-
By theorem (2),
$\dfrac{\mathrm{ar}\left(\triangle\mathrm{ABC}\right)}{\mathrm{ar}\left(\triangle\mathrm{XBY}\right)}=\left(\dfrac{\mathrm{AB}}{\mathrm{XB}}\right)^2\\\mathrm{By}\;\mathrm{equation}\left(3\right),\\\left(\dfrac{\mathrm{AB}}{\mathrm{XB}}\right)^2=2\\\dfrac{\mathrm{AB}}{\mathrm{XB}}=\sqrt2\\\mathrm{BX}=\mathrm{AB}-\mathrm{AX}\\\dfrac{\mathrm{AB}-\mathrm{AX}}{\mathrm{AB}}=\dfrac1{\sqrt2}\\1-\dfrac{\mathrm{AX}}{\mathrm{AB}}=\dfrac1{\sqrt2}\\\dfrac{\mathrm{AX}}{\mathrm{AB}}=1-\dfrac1{\sqrt2}=\dfrac{\sqrt2-1}{\sqrt2}\\\dfrac{\mathrm{AB}}{\mathrm{AX}}=\dfrac{\sqrt2}{\sqrt2-1}$
Hence the ratio of AX and AB is $\sqrt2-1:\sqrt2$

Note:To solve this problem, one should have a knowledge of similarity of triangles and ratios. Be sure to change the answer into ratio form. Do not assume the triangles to be similar. Prove the similarity by AA similarity.