Question

In triangle ABC the co-ordinates of vertices A, B and C are \[\left( {4,7} \right),\left( { - 2,3} \right)\] and \[\left( {0,1} \right)\] respectively. Find the equations of medians passing through vertices A, B and C.
The question has multiple correct options
A. \[x - y + 3 = 0\]
B. \[x - 4y + 14 = 0\]
C. \[x + y + 3 = 0\]
D. \[4x - y + 1 = 0\]

Answer 1

Hint: First of all, consider the median points and draw the figure accordingly. Then find each mid-point of the lines in triangle ABC. The equation of the median is given by the line joining the mid-point and its opposite point. So, use this concept to reach the solution to the given problem.

Complete step-by-step solution:
Given points are \[A\left( {4,7} \right),B\left( { - 2,3} \right),C\left( {0,1} \right)\].
Let the medians of the triangle ABC are D, E, F on the sides AB, BC, CA respectively as shown in the below figure:

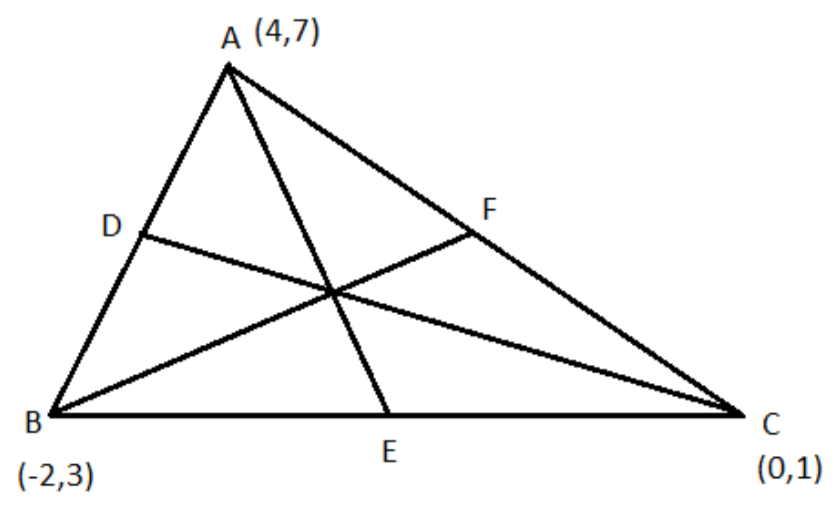
We know that the midpoint of the points \[\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)\] is given by \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\].
So, the mid-point of AB is \[D = \left( {\dfrac{{4 - 2}}{2},\dfrac{{7 + 3}}{2}} \right) = \left( {1,5} \right)\]
The mid-point of BC is \[E = \left( {\dfrac{{ - 2 + 0}}{2},\dfrac{{3 + 1}}{2}} \right) = \left( { - 1,2} \right)\]
The mid-point of CA is \[F = \left( {\dfrac{{4 + 0}}{2},\dfrac{{7 + 1}}{2}} \right) = \left( {2,4} \right)\]
We know that the equation of the line joining the two point \[\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)\] is given by \[\left( {y - {y_1}} \right) = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)\].
The equation of median passing through A and midpoint of BC i.e., E is given by
\[ \Rightarrow y - 7 = \dfrac{{2 - 7}}{{ - 1 - 4}}\left( {x - 4} \right) \\
   \Rightarrow y - 7 = \dfrac{{ - 5}}{{ - 5}}\left( {x - 4} \right) \\
   \Rightarrow \left( {y - 7} \right) = 1\left( {x - 4} \right) \\
   \Rightarrow y - 7 = x - 4 \\
  \therefore x - y + 3 = 0 \\ \]
The equation of median passing through B and mid-point CA i.e., F is given by
\[ \Rightarrow y - 3 = \dfrac{{4 - 3}}{{2 + 2}}\left( {x + 2} \right) \\
   \Rightarrow y - 3 = \dfrac{1}{4}\left( {x + 2} \right) \\
   \Rightarrow 4\left( {y - 3} \right) = 1\left( {x + 2} \right) \\
   \Rightarrow 4y - 12 = x + 2 \\
  \therefore x - 4y + 14 = 0 \\ \]
The equation of median passing through C and mid-point AB i.e., D is given by
\[ \Rightarrow y - 1 = \dfrac{{5 - 1}}{{1 - 0}}\left( {x - 0} \right) \\
   \Rightarrow y - 1 = \dfrac{4}{1}\left( x \right) \\
   \Rightarrow 1\left( {y - 1} \right) = 4x \\
   \Rightarrow y - 1 = 4x \\
  \therefore 4x - y + 1 = 0 \\ \]
Thus, the correct options are A, B and D.

Note:The equation of the line joining the two point \[\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)\] is given by \[\left( {y - {y_1}} \right) = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\left( {x - {x_1}} \right)\]. The midpoint of the points \[\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)\] is given by \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\].