Question

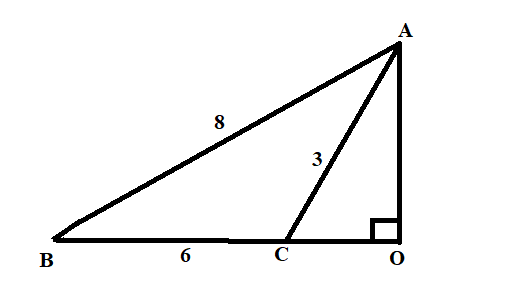
In triangle ABC, given below AB = 8 cm BC = 6 cm and AC = 3 cm. Calculate the length of OC.

a) 2 cm
b) 3.32 cm
c) 1.58 cm
d) 1 cm

Answer 1

Hint: For solving this question, first we let the length of AO be y and CO be x. Now, we apply Pythagoras theorem in the right-angled triangle AOC and get an equation in terms of x and y. Again, applying Pythagoras theorem in a right-angle triangle AOB and with the help of the previous equation, we find the length of OC.
Complete step-by-step answer:
In mathematics, the Pythagoras Theorem states that "In a right-angle triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides". Applying Pythagoras theorem in right-angle triangle AOC, we get:
$A{{O}^{2}}+O{{C}^{2}}=A{{C}^{2}}$
Let, the length of AO be ‘y’ cm and the length of OC be ‘x’ cm. After putting x and y in the above expression, we get equation (1) as:
$\begin{align}
  & \Rightarrow {{y}^{2}}+{{x}^{2}}={{3}^{2}} \\
 & \therefore {{y}^{2}}={{3}^{2}}-{{x}^{2}}....\left( 1 \right) \\
\end{align}$
Similarly, applying Pythagoras theorem in right angle triangle AOB where AO is y and OB is (x + 6), we have equation (2) as:
$\begin{align}
  & A{{O}^{2}}+O{{B}^{2}}=A{{B}^{2}} \\
 & \Rightarrow {{y}^{2}}+{{\left( x+6 \right)}^{2}}={{8}^{2}}\ldots (2) \\
\end{align}$
Putting the value of ${{y}^{2}}$ from the equation (1) and using the algebraic expansion of ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$, we have
$\begin{align}
  & \Rightarrow 9-{{x}^{2}}+{{x}^{2}}+12x+36=64 \\
 & \Rightarrow 12x+45=64 \\
 & \Rightarrow 12x=64-45=19 \\
 & \Rightarrow x=\dfrac{19}{12} \\
 & \Rightarrow x=1.58cm \\
\end{align}$
Hence, the length of OC is 1.58cm.
Therefore, option (c) is correct.
Note: Students must remember the application of Pythagoras theorem in a right-angled triangle to obtain the answer for this problem. Only right-angle triangles must be chosen for applying Pythagoras theorem and not triangle ABC.