Question

In triangle ABC, angle C is the right angle and angle B is \[{30^ \circ }\]. What is the ratio of AC to BC?

Answer 1

Hint: This question is simply based on the basic trigonometric functions. We will first draw a basic triangle from the data so given. Then using the sin function we will find the ratio of the sides. We will find the ratios in terms of hypotenuse so that on equating the fractions we will get the required ratio easily.

Complete step-by-step answer:
Given that, In triangle ABC, angle C is the right angle and angle B is \[{30^ \circ }\]. Since the sum of all angles of a triangle is \[{180^ \circ }\] the given triangle will be \[{30^ \circ } - {60^ \circ } - {90^ \circ }\]. Thus remaining angle id of \[{60^ \circ }\]

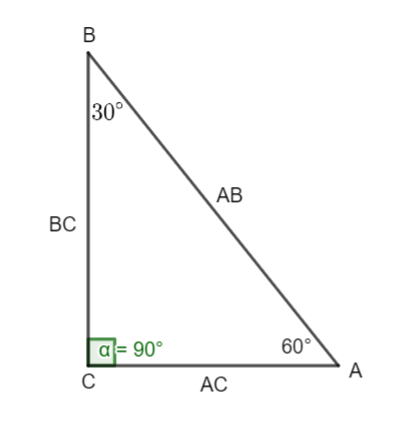
Now we will start towards the ratio process.
As we know that sin is the function in trigonometry valued as ratio of opposite side to hypotenuse.
\[\sin {30^ \circ } = \dfrac{{AC}}{{AB}}\]
\[AB = \dfrac{{AC}}{{\operatorname{Sin} {{30}^ \circ }}}\]
As we know the value of \[\operatorname{Sin} {30^ \circ } = \dfrac{1}{2}\]. Thus the ratio above becomes,
\[AB = 2AC\]
Now for the next ratio,
\[\sin {60^ \circ } = \dfrac{{BC}}{{AB}}\]
\[AB = \dfrac{{BC}}{{\sin {{60}^ \circ }}}\]
We know that, \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}\]
\[AB = \dfrac{{2BC}}{{\sqrt 3 }}\]
Since LHS of both the fraction is same we can equate them as
\[2AC = \dfrac{{2BC}}{{\sqrt 3 }}\]
Taking the ratio of respective sides,
\[\dfrac{{AC}}{{BC}} = \dfrac{1}{{\sqrt 3 }}\]
This is the correct answer.

Note: Note that, when we solve this problem there is no need of using any identity or working with any complex tough tricks. But the only thing we should note is that it is a \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] triangle. And we are familiar with the basic values of these angles and their respective functions. And this is the key factor to solve the problem above. We also can solve or find the fractions with side AB that is the hypotenuse of the triangle above.