
In triangle ABC $AB=AC$ and $\angle B=\angle C$ , prove that $\Delta ABE\approx \Delta ACD$ .

Answer
531.3k+ views
Hint: Here in this question we have been asked to prove that $\Delta ABE\approx \Delta ACD$ , when it is given as $AB=AC$ and $\angle B=\angle C$ in $\Delta ABC$ . For answering this question we are going to use the Angle-Side-Angle congruence theorem concept.
Complete step-by-step solution:
Now considering from the question we have been asked to prove that $\Delta ABE\approx \Delta ACD$ , when it is given as $AB=AC$ and $\angle B=\angle C$ in $\Delta ABC$ .
From the basic concepts we know that we have different concurrence theorems like Angle-Side-Angle or Side-Angle-Side and many more which we have learnt during the concept of congruence of triangles.
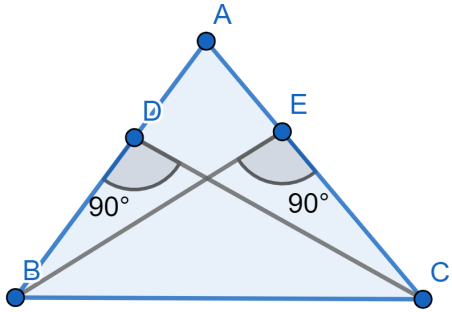
From the given figure we can say that $BE$ and $CD$ are perpendiculars of $\Delta ABC$ . Hence we can say that these angles $\angle ADC,\angle BDC,\angle AEB,\angle CEB$ are right angles.
We can consider in the triangle $\Delta ABE$ , $\angle BAE$ which would be equal to the $\angle A$ in the main triangle $\Delta ABC$ and $\angle AEB={{90}^{\circ }}$. In the triangle $\Delta ABE$ , $AB$ is a side which is equal to $AC$.
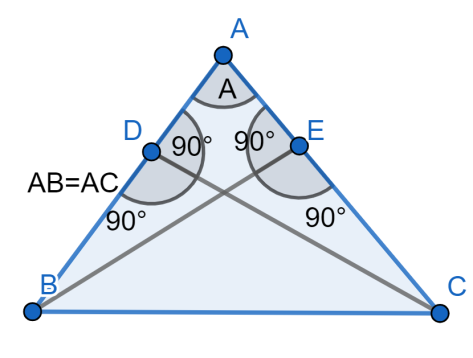
We can consider in the triangle $\Delta ACD$ , $\angle DAC$ which would be equal to the $\angle A$ in the main triangle $\Delta ABC$ and $\angle ADC={{90}^{\circ }}$ . In the triangle $\Delta ACD$ ,$AC$ is a side which is equal to $AB$.
As 2 angles $\angle BAE=\angle DAC$ and $\angle AEB=\angle ADC$ a side $AB=AC$ are same we can say that $\Delta ABE\approx \Delta ACD$ using Angle-Side-Angle congruence.
Hence we can conclude that $\Delta ABE\approx \Delta ACD$ is proved, when it is given as $AB=AC$ and $\angle B=\angle C$ in $\Delta ABC$.
Note: While answering questions of this type we should be sure with the concepts that we are going to apply in between the process. Some of us can consider that when 2 angles are the same in the corresponding triangles the other angle will also be the same because the sum of all angles in a triangle is always equal to ${{180}^{\circ }}$ . As 3 angles are equal they will conclude they are congruent but this is not right in all the cases so we don’t have Angle-Angle-Angle congruence in the theorems.
Complete step-by-step solution:
Now considering from the question we have been asked to prove that $\Delta ABE\approx \Delta ACD$ , when it is given as $AB=AC$ and $\angle B=\angle C$ in $\Delta ABC$ .

From the basic concepts we know that we have different concurrence theorems like Angle-Side-Angle or Side-Angle-Side and many more which we have learnt during the concept of congruence of triangles.
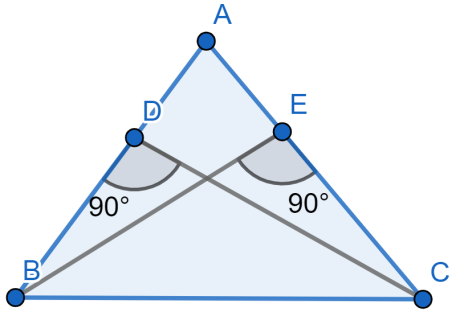
From the given figure we can say that $BE$ and $CD$ are perpendiculars of $\Delta ABC$ . Hence we can say that these angles $\angle ADC,\angle BDC,\angle AEB,\angle CEB$ are right angles.
We can consider in the triangle $\Delta ABE$ , $\angle BAE$ which would be equal to the $\angle A$ in the main triangle $\Delta ABC$ and $\angle AEB={{90}^{\circ }}$. In the triangle $\Delta ABE$ , $AB$ is a side which is equal to $AC$.

We can consider in the triangle $\Delta ACD$ , $\angle DAC$ which would be equal to the $\angle A$ in the main triangle $\Delta ABC$ and $\angle ADC={{90}^{\circ }}$ . In the triangle $\Delta ACD$ ,$AC$ is a side which is equal to $AB$.
As 2 angles $\angle BAE=\angle DAC$ and $\angle AEB=\angle ADC$ a side $AB=AC$ are same we can say that $\Delta ABE\approx \Delta ACD$ using Angle-Side-Angle congruence.
Hence we can conclude that $\Delta ABE\approx \Delta ACD$ is proved, when it is given as $AB=AC$ and $\angle B=\angle C$ in $\Delta ABC$.
Note: While answering questions of this type we should be sure with the concepts that we are going to apply in between the process. Some of us can consider that when 2 angles are the same in the corresponding triangles the other angle will also be the same because the sum of all angles in a triangle is always equal to ${{180}^{\circ }}$ . As 3 angles are equal they will conclude they are congruent but this is not right in all the cases so we don’t have Angle-Angle-Angle congruence in the theorems.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which places in India experience sunrise first and class 9 social science CBSE

Who is eligible for RTE class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




