Question

In triangle ABC, AB = AC, $\text{BD}\bot \text{AC}$ and $\text{CF}\bot \text{AB}$, then BA = CF.
If the above statement is true then mention the answer as 1, else mention 0 if false.

Answer 1

Hint: Here, first we will draw the diagram according to the conditions mentioned in the question. Now, we will consider one of the triangles and according to the Pythagorean theorem and basics of right-angled triangle properties. Use the obtained conditions to compare with one of the given conditions, to find whether the statement is true or false.

Complete step by step answer:
Here, in this question, let us first draw the triangle with all the conditions which are given in the question.

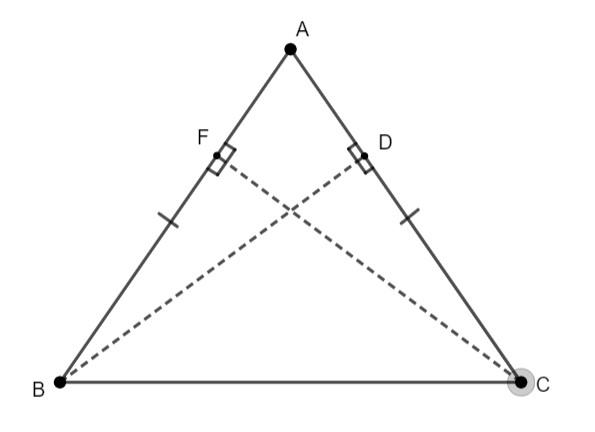
Here, we have AB = AC, which makes the triangle ABC an isosceles triangle. Next given condition is that $\text{BD}\bot \text{AC}$ and $\text{CF}\bot \text{AB}$, now we have to check if BA = CF.
First, due to the perpendicular bisectors BD and CF, we have triangles CFA, CFB, BDC and BDA.
For the required proof, we will consider two triangles, triangle CFA and triangle ABC.
From the triangle CFA, we can see that $\text{CF}\bot \text{AB}$ therefore, $\angle \text{F=90}{}^\circ $.
Therefore, we can say that triangle CFA is a right-angled triangle.
By Pythagorean theorem and basics of a right-angled triangle,
we can say that AC > CF ............. (1)
Now, from triangle ABC, we have from the given conditions,
AB = AC ............... (2)
From equations (1) and (2), we get
AB > CF
The above condition proves that side BA is greater than side CF and not equal.

Therefore, the given statement is false, hence we will choose 0.

Note: Here, in this question, while considering the triangle CFA, AC is considered to be greater than CF because AC is the hypotenuse of the right-angled triangle CFA and hypotenuse is the longest side in a right-angled triangle.