Question

In triangle ABC, AB = AC = 10 cm. $\angle ABC = 50^\circ $.
(a).Find the length of BC
(b).Find the diameter of the circle.
$\left[ {\sin 50^\circ = 0.77,{\text{ }}\cos 50^\circ = 0.64,{\text{ }}\tan 50^\circ = 1.19} \right]$

Answer 1

Hint: As the given triangle is an isosceles triangle, using angle sum property we can determine all the angles in the triangle. Using the trigonometric ratios we can determine the value of BC. And to determine the diameter of the circle, we need to find the circumradius using Area=$\dfrac{{abc}}{{4R}}$, where a, b, c are sides of the triangle. Where Area can be determined using the formula, Area ($\vartriangle ABC$) =$$\dfrac{1}{2} \times $$base$ \times $height.
Complete step by step answer:
Consider the given figure:
Since, AB = AC = 10 cm, $\vartriangle ABC$is an isosceles triangle and hence the base angles are equal.
i.e. $\angle B = \angle C = 50^\circ $… (1)
Angle sum property of triangle states that the sum of interior angles of a triangle is $180^\circ $.
By angle sum property, we have$\angle A + \angle B + \angle C = 180^\circ $
$ \Rightarrow \angle A + 50^\circ + 50^\circ = 180^\circ $ [From (1)]
$ \Rightarrow \angle A + 100^\circ = 180^\circ $
$$ \Rightarrow \angle A = 180^\circ - 100^\circ = 80^\circ $$
The perpendicular from the vertex of an isosceles triangle to the base bisects the base.

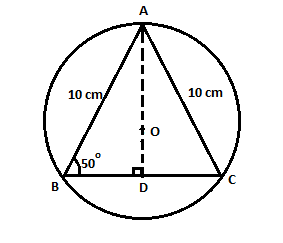
(a).Consider the right triangle$\vartriangle ABD$:
$\cos 50^\circ $=$\dfrac{{BD}}{{AB}} \Rightarrow 0.64 = \dfrac{{BD}}{{10}}$ (Since$\cos \theta = \dfrac{{adj.side}}{{hyp}}$)
$ \Rightarrow BD = 6.4cm$
We have, BC = BD + DC = $2 \times BD$=$2 \times 6.4$=12.8 cm
(b).From the figure, it is clear that OA = OB = OC is the circumradius of$\vartriangle ABC$.
Let A be the area of$\vartriangle ABC$and let R be the circumradius.
Let a, b, c denote the triangle’s three sides and let A denote the area of the triangle. The measure of the circumradius of the triangle is simply R =$\dfrac{{abc}}{{4A}}$. This can be rewritten as A =$\dfrac{{abc}}{{4R}}$
We know that A =$\dfrac{{abc}}{{4R}}$, where a, b, c are the sides of the triangle.
From$\vartriangle ABC$,
$\tan 50^\circ = \dfrac{{AD}}{{BD}} \Rightarrow 1.19 = \dfrac{{AD}}{{6.4}}$
$ \Rightarrow AD = 1.19 \times 6.4 = 7.616{\text{ cm}}$
Area ($\vartriangle ABC$) = $$\dfrac{1}{2} \times $$base$ \times $height
$ \Rightarrow \dfrac{1}{2} \times {\text{BC}} \times {\rm A}{\text{D}}$
$ \Rightarrow \dfrac{1}{2} \times 12.8 \times 7.616 = 48.7424$sq.cm
Since, A =$\dfrac{{abc}}{{4R}}$, we have R =$\dfrac{{abc}}{{4A}}$
$ \Rightarrow \dfrac{{10 \times 10 \times 12.8}}{{4 \times 48.7424}} = 6.57 {\text{cm}}$
Thus, diameter of the circle = 2R = 2$ \times $6.57 = 13.14 cm

Note: Formula for Circumradius can be given by R =$\dfrac{{abc}}{{4rs}}$where R is the circumradius, r is the inradius, and a, b, and c are the respective sides of the triangle and s =$\dfrac{{\left( {a + b + c} \right)}}{2}$is the semi perimeter. To find the area of the triangle by Heron’s formula: A =$\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $