Question

In trapezium PQRS, side PQ is parallel to side SR and AR=5AP and also AS=5AQ, then prove that SR=5PQ.

Answer 1

Hint: First, we know from the study of parallel lines that in between two parallel lines if any transverse line cuts both the lines then the angles made by that lines are always equal. Then, by using the same concept to the given lines which are parallel PQ and RS, so in $\Delta APQ$and $\Delta ARS$, we get these triangles as congruent and similar. Then, by using the AAA property of congruency, we get $\Delta APQ$and $\Delta ARS$as congruent and similar. Then, by using the above conclusion that $\Delta APQ$and $\Delta ARS$are similar, we also know that for similar triangles, the ratio of the respective sides of the triangle is always the same which gives the final result.

Complete step by step answer:
In this question, we are supposed to prove that SR=5PQ, when PQRS is a trapezium with side PQ, is parallel to side SR and AR=5AP and also AS=5AQ.
So, before proceeding for this, we must understand the figure that side PQ is parallel with side SR and other conditions in a trapezium PQRS with center A as:

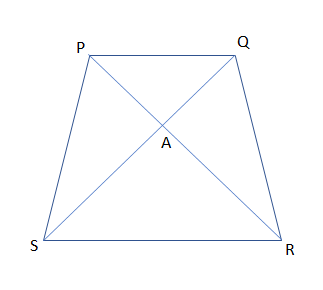
Now, we know from the study of parallel lines that in between two parallel lines if any transverse line cuts both the lines then the angles made by that lines are always equal.
So, by using the same concept to the given lines which are parallel PQ and RS, so in $\Delta APQ$and $\Delta ARS$, we get:
$\angle QPA=\angle ARS$(alternate interior angle)
$\angle AQP=\angle ASR$(alternate interior angle)
$\angle PAQ=\angle SAR$(vertically opposite angle)
So, by using the AAA property of congruency, we get $\Delta APQ$and $\Delta ARS$as congruent and similar. Then, by using the above conclusion that $\Delta APQ$and $\Delta ARS$are similar, we also know that for similar triangles, the ratio of the respective sides of the triangle is always the same.
So, by using the above concept, we get:
$\dfrac{AP}{AR}=\dfrac{PQ}{SR}=\dfrac{AQ}{AS}$
Now, we are given in the question the condition that AR=5AP and by substituting this value in the above expression, we get:
$\begin{align}
  & \dfrac{AP}{5AP}=\dfrac{PQ}{SR} \\
 & \Rightarrow \dfrac{PQ}{SR}=\dfrac{1}{5} \\
 & \Rightarrow SR=5PQ \\
\end{align}$
So, we get the condition that SR=5PQ.
Hence, the given condition is proved.

Note:
 Now, to solve these types of questions we need to know some of the basics of the concept of parallel lines intersected by a traverse line as in the above question the diagonal are intersecting the parallel sides PQ and RS. So, we get all the interior angles as equal in between parallel lines when it is intersected by a straight transverse line.